论文背景
在分析一个复杂物理系统时,常见的问题是不能直接测量我们感兴趣的系统参数。对于许多这样的系统,科学家们已经发展出复杂的理论来解释,测量值y是如何从隐藏的系统参数x中产生的。我们将把这种映射称为前向过程。然而,其逆过程需要从测量中推断出系统的隐藏状态。然而,因为关键信息在正向过程中丢失了,逆过程是不适定问题(ill-posed,即许多种系统参数x都可产生同一个测量值y)。
给定一个测量值时,这种逆过程的解往往有多个,所以作者提出,解决逆过程时,必须给出一个在以某个观察为条件的,系统参数的条件后验概率分布,即\(p(\mathbf{x|y})\)。针对这一任务本文提出了可逆神经网络(invertible neural networks, INNs)。
可逆神经网络有3个特点:
- 输入到输出是双射的(bijective),即他的逆存在。
- 前向映射和逆映射都是可以被有效计算的。
- 两个映射都有一个可处理的雅可比矩阵,允许显式地计算后验概率。
因此就可以只训练一个易于理解的前向过程,即可在预测过程中计算反向过程。
为了抵消前向过程的固有信息损失,引入了额外的潜在输出变量\(\mathbf z\),它捕获了\(\mathbf y\)中的不包含的关于x的信息。即INN把输入\(\mathbf x\)与一个二元组\([\mathbf y,\mathbf z]\)联系在一起。前向过程为\([\mathbf{y}, \mathbf{z}]=f(\mathbf{x})\);逆过程为\(\mathbf{x}=f^{-1}(\mathbf{y}, \mathbf{z})=g(\mathbf{y}, \mathbf{z})\)。
另外,INN保证\(\mathbf z\)的分布是一个高斯分布。这样就能把待求的分布\(p(\mathbf{x|y})\)用一个确定的函数\(\mathbf{x}=g(\mathbf{y}, \mathbf{z})\)把\(\mathbf z\)的高斯分布\(p(\mathbf z)\)转换到\(\mathbf x\)空间上,并且以\(\mathbf y\)作为条件。
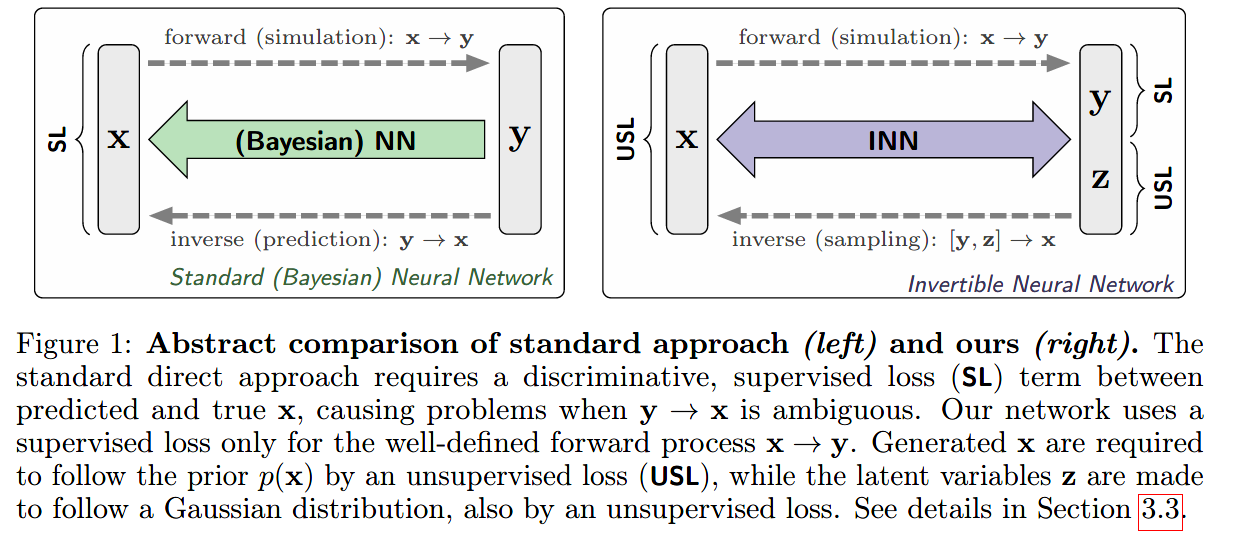
如上图所示,是在学习逆过程汇总,传统网络与本文提出的可逆网络的对比。
- 左边的图是代表用通常的网络去学习逆过程,使用一个真实\(\mathbf x\)与预测\(\hat {\mathbf x}\)之间的监督损失(supervised loss,SL)来约束。
- 右边的图是使用INN去学习逆过程,在两个方向上都有loss
方法详述
问题描述
研究人员对描述某一现象的一组参数\(\mathbf{x} \in \mathbb{R}^{D}\)感兴趣,但是却观测不到。能观测到的是\(\mathbf{y} \in \mathbb{R}^{M}\)。对应的理论已经能提供一个模型\(\mathbf{y}=s(\mathbf{x})\)来描述这一前向过程了。但是由\(\mathbf x\)到\(\mathbf y\)的转换过程中遭受了信息损失,即\(\mathbf y\)的本征维度(intrinsic dimension)小于\(D\)。因此,把逆过程建模成一个条件概率模型:\(p(\mathbf{x} \mid \mathbf{y})\)
我们的目标就是,使用由前向过程\(s\)以及一个\(\mathbf x\)的先验\(p(\mathbf x)\),构造的数据集\(\left\{\left(\mathbf{x}_{i}, \mathbf{y}_{i}\right)\right\}_{i=1}^{N}\),学习一个模型\(q(\mathbf{x} \mid \mathbf{y})\)去拟合这个\(p(\mathbf{x} \mid \mathbf{y})\)。
对于这样的数据集,其实也可以训练一个标准的回归模型。但是我们的目的是拟合一个完整的概率分布,为此,我们引入了一个符合标准正态分布的隐变量\(\mathbf{z} \in \mathbb{R}^{K}\),从而把\(q(\mathbf{x} \mid \mathbf{y})\)重新参数化为一个输入为\(\mathbf y\)与\(\mathbf z\),输出\(\mathbf x\)的一个确定函数\(g\),其中\(g\)的参数为\(\theta\): \[ \mathbf{x}=g(\mathbf{y}, \mathbf{z} ; \theta) \quad \text { with } \quad \mathbf{z} \sim p(\mathbf{z})=\mathcal{N}\left(\mathbf{z} ; 0, I_{K}\right) \] 值得注意的是,\(\mathbf x\)是代表现实世界中不可观察的属性;而\(\mathbf z\)是为我们的模型携带一个固有的信息。非线性独立分量分析理论(non-lineari ndependent component analysis )证明,一个高斯先验对z没有额外的限制。(?这段我不是太理解)
与常规的神经网络方法相对比,我们不是直接学习\(\mathbf{x}=g(\mathbf{y}, \mathbf{z} ; \theta)\)这一映射,而是通过把其逆过程\(f(\mathbf{x} ; \theta)\)拟合为原始的前向过程\(s(\mathbf x)\): \[ [\mathbf{y}, \mathbf{z}]=f(\mathbf{x} ; \theta)=\left[f_{\mathbf{y}}(\mathbf{x} ; \theta), f_{\mathbf{z}}(\mathbf{x} ; \theta)\right]=g^{-1}(\mathbf{x} ; \theta) \quad \text { with } \quad f_{\mathbf{y}}(\mathbf{x} ; \theta) \approx s(\mathbf{x}) \] \(f=g^{-1}\)是由INN的网络结构保证的。
值得一提的是,设\(\mathbf y\)的本征维数为\(m\le M\),则需要隐变量\(\mathbf z\)的维度为\(K=D-m\)。如果\(m<M\)时,则\(\mathbf y\)的实际维度\(M\)加上\(\mathbf z\)的维度\(K\)则大于了原始的\(\mathbf x\)的维度\(D\),那么就给原始的\(\mathbf x\)加上一些值为0的维度\(\mathbf{x}_{0} \in \mathbb{R}^{M+K-D}\),以\([\mathbf{x},\mathbf{x_0}]\)作为输入即可。
这里复习一个概率论的简单知识,已知随机变量\(X \sim P_{X}(x), Y=f(X)\),求 \(Y\) 的概率密度函数 \(P_{Y}(y)\):
解:当 \(f\) 为递增函数时, 考察 Y 的累计分布函数 \(F_{Y}(y)\) : \[ F_{Y}(y)=\operatorname{Pr}(Y \leq y)=\operatorname{Pr}\left(X \leq f^{-1}(y)\right)=F_{X}\left(f^{-1}(y)\right) \] 故 \[ P_{Y}(y)=\frac{d F_{Y}(y)}{d y}=P_{X}\left(f^{-1}(y)\right) \frac{d f^{-1}(y)}{d y} \] 当 f 为递减函数时, \[ F_{Y}(y)=\operatorname{Pr}(Y \leq y)=\operatorname{Pr}\left(X \geq f^{-1}(y)\right)=1-F_{X}\left(f^{-1}(y)\right) \] 故 \[ P_{Y}(y)=\frac{d F_{Y}(y)}{d y}=-P_{X}\left(f^{-1}(y)\right) \frac{d f^{-1}(y)}{d y} \] 综上所述, \[ P_{Y}(y)=\frac{d F_{Y}(y)}{d y}=P_{X}\left(f^{-1}(y)\right)\left|\frac{d f^{-1}(y)}{d y}\right|=\frac {P_{X}\left(f^{-1}(y)\right)}{\left|\left.\frac{d f(x)}{d x}\right|_{f^{-1}(y)}\right|} \]
容易把\(q(\mathbf x|\mathbf y)\)写为:
\[ q(\mathbf{x}=g(\mathbf{y}, \mathbf{z} ; \theta) \mid \mathbf{y})=p(\mathbf{z})\left|J_{\mathbf{x}}\right|^{-1}, \quad J_{\mathbf{x}}=\operatorname{det}\left(\left.\frac{\partial g(\mathbf{y}, \mathbf{z} ; \theta)}{\partial[\mathbf{y}, \mathbf{z}]}\right|_{\mathbf{y}, f_{\mathbf{z}}(\mathbf{x})}\right) \]
\(J_{\mathbf{x}}\)为雅克比行列式。
可逆的网络结构
这里作者使用了2016年Real NVP中提出的结构(https://arxiv.org/pdf/1605.08803)。这种网络的基本单元是由两个互补的仿射耦合层组成的可逆块。
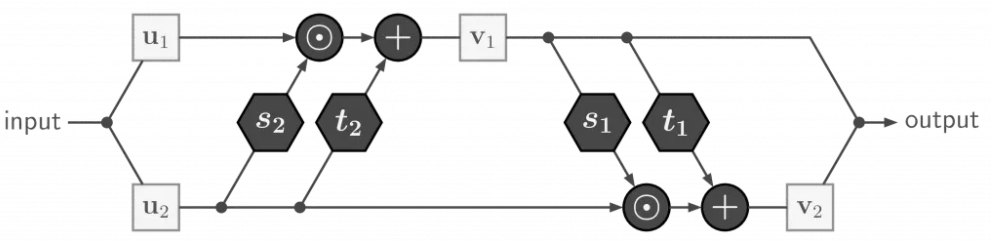
在前向过程对于输入的向量\(\mathbf u\),拆分为两等分\(\mathbf u_1\)与\(\mathbf u_2\),分别通过由\(\exp \left(s_{i}\right)\)和\(t_{i}\)(\(i \in\{1,2\}\),即两层)决定系数的仿射映射层: \[
\mathbf{v}_{1}=\mathbf{u}_{1} \odot \exp \left(s_{2}\left(\mathbf{u}_{2}\right)\right)+t_{2}\left(\mathbf{u}_{2}\right), \quad \mathbf{v}_{2}=\mathbf{u}_{2} \odot \exp \left(s_{1}\left(\mathbf{v}_{1}\right)\right)+t_{1}\left(\mathbf{v}_{1}\right)
\] 
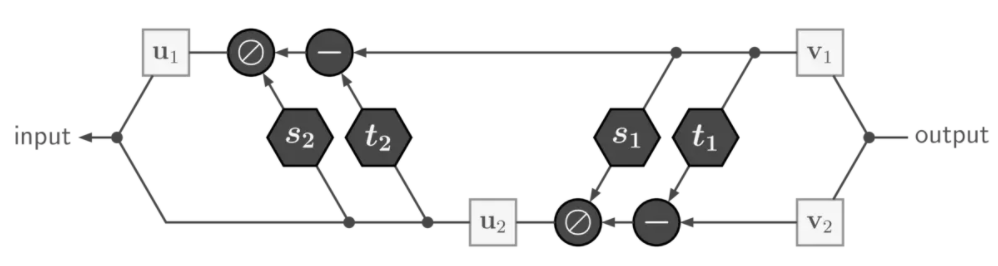
而对于上式,如果给定\(\mathbf{v}=\left[\mathbf{v}_{1}, \mathbf{v}_{2}\right]\),容易得到其逆过程: \[
\mathbf{u}_{2}=\left(\mathbf{v}_{2}-t_{1}\left(\mathbf{v}_{1}\right)\right) \odot \exp \left(-s_{1}\left(\mathbf{v}_{1}\right)\right), \quad \mathbf{u}_{1}=\left(\mathbf{v}_{1}-t_{2}\left(\mathbf{u}_{2}\right)\right) \odot \exp \left(-s_{2}\left(\mathbf{u}_{2}\right)\right)
\] 
最重要的是,\(s_i\)和\(t_i\)的映射可以是任意复杂的\(\mathbf v_1\)和\(\mathbf u_2\)的函数,它们本身不需要是可逆的。在本文的实现中,它们是通过一系列全连接层+Leaky ReLU激活函数组成的。
对于这种网络结构,作者在实际使用的时候加了两个小扩展:
- 这种映射方式,是无法改变向量的维数的。当输入的维度\(D\)过小而不足以满足复杂的映射关系时,可以在输入端(对于逆过程则是输出端)扩展一些值为0的维度来实现维度的增加。而“扩展一些值为0的维度”这一操作,是不会改变向量的本征维度的。
- 在各个上述的基本单元之间,加入一些层,这些层的操作是以固定的操作打乱输入向量的各个元素的排列。这使得\(\mathbf{u}=\left[\mathbf{u}_{1}, \mathbf{u}_{2}\right]\)的操作在不同层之间是变化的,从而增强元素之间的相互作用。
双向训练过程
可逆网络使得训练过程中可以以交替的方式执行前向和逆向迭代,从两个方向进行梯度传播,进而进行参数更新。从而有三个损失函数,其中\(\mathcal{L_y}\)、\(\mathcal{L_z}\)是针对前向传播的损失函数;而\(\mathcal{L_x}\)是针对逆向传播的损失函数。
损失函数\(\mathcal{L_y}\)
这个损失函数是对实际前向过程\(\mathbf{y}_{i}=s\left(\mathbf{x}_{i}\right)\)与网络预测值\(f_{\mathbf{y}}\left(\mathbf{x}_{i}\right)\)进行约束,即\(\mathcal{L}_{\mathbf{y}}\left(\mathbf{y}_{i}, f_{\mathbf{y}}\left(\mathbf{x}_{i}\right)\right)\),这个非常好理解。之所以下标为\(\mathbf y\),是对网络中与\(\mathbf y\)生成有关的参数进行更新。\(\mathcal{L_y}\)的形式可以是任意的监督损失,比如回归中的平方损失、或是分类中的交叉熵损失。
损失函数\(\mathcal{L_z}\)
对于与隐变量\(\mathbf z\)生成有关的网络参数,使用一个损失函数\(\mathcal{L_z}\),这个损失函数要让“网络输出的\(\mathbf y,\mathbf z\)的联合概率分布”与“训练数据中的\(\mathbf y\)的分布\(p(\mathbf y)\)与\(\mathbf z\)的期望的分布\(p(\mathbf z)\)的乘积”尽可能一致。直观上,这个损失函数不仅要使得网络生成的\(\mathbf z\)的分布尽可能为\(p(\mathbf z)\),而且使\(\mathbf y\)与\(\mathbf z\)是独立的(即不能让\(\mathbf y\)与\(\mathbf z\)编码了同样的信息)。
形式上写为:\(\mathcal{L}_{\mathbf{z}}(q(\mathbf{y}, \mathbf{z}), p(\mathbf{y}) p(\mathbf{z}))\)
\(q(\mathbf{y}, \mathbf{z})\)为网络输出的联合概率分布,实际上\(q\left(\mathbf{y}=f_{\mathbf{y}}(\mathbf{x}), \mathbf{z}=f_{\mathbf{z}}(\mathbf{x})\right)=p(\mathbf{x}) /\left|J_{\mathbf{y z}}\right|\),其中\(J_{\mathbf{y z}}=\operatorname{det}\left(\left.\frac{\partial f(\mathbf x ; \theta)}{\partial\mathbf x}\right|_{g(\mathbf{y}, \mathbf z)}\right)\)。
\(p(\mathbf y)\)为训练数据的\(\mathbf y\)的分布。因为训练数据中的\(\mathbf y_i\)是由前向模型\(\mathbf y_i=s(\mathbf x_i)\)生成的,所以实际上满足\(p(\mathbf{y}=s(\mathbf{x}))=p(\mathbf{x}) / \left| J_{s}\right|\),其中\(J_s=\operatorname{det}\left(\left.\frac{\partial s(\mathbf x )}{\partial\mathbf x}\right|_{s^{-1}(\mathbf y)}\right)\).
但是,这里作者使用了最大均值差异(Maximum Mean Discrepancy,MMD)的方法来实现\(\mathcal{L_z}\),从而只需要从分布中采样即可作比较,而不需要显式地计算两个雅克比行列式\(J_s\)与\(J_{\mathbf {yz}}\)。具体MMD的方法在后面介绍。
对于以上两个损失函数。作者证明了一个定理:
Theorem: If an \(I N N f(\mathbf{x})=[\mathbf{y}, \mathbf{z}]\) is trained as proposed, and both the supervised loss \(\mathcal{L}_{\mathbf{y}}=\mathbb{E}\left[\left(\mathbf{y}-f_{\mathbf{y}}(\mathbf{x})\right)^{2}\right]\) and the unsupervised loss \(\mathcal{L}_{\mathbf{z}}=D(q(\mathbf{y}, \mathbf{z}), p(\mathbf{y}) p(\mathbf{z}))\) reach zero, sampling \(g\) according to \(E q .\) 1 with \(g=f^{-1}\) returns the true posterior \(p\left(\mathbf{x} \mid \mathbf{y}^{*}\right)\) for any measurement \(\mathbf{y}^{*}\).
证明过程:
损失函数\(\mathcal{L_x}\)
虽然定理表明\(\mathcal{L_y}\)、\(\mathcal{L_z}\)基本已经够用了,但是因为训练的迭代次数毕竟是有限的,因此\(\mathbf y\)和\(\mathbf z\)之间仍然存在少量残留的依赖关系,这使得\(q(\mathbf{x} \mid \mathbf{y})\)难以准确拟合\(p(\mathbf{x} \mid \mathbf{y})\)。为了加速收敛,作者又提出了一个\(\mathcal{L_x}\)。
直观上解释,这个loss就是把原本的\(\mathbf x\)代入网络前向传播,得到\(\mathbf y\)与\(\mathbf z\),然后把得到的分布\(p(\mathbf y)\)与\(p(\mathbf z)\)看做独立的,分别在其中采样,并逆向传播回来,得到分布\(q(\mathbf x)\),使其尽量和原始的\(p(\mathbf x)\)相似(这个拟合过程的loss也是使用MMD实现的):
形式化地表示为:\(\mathcal{L}_{\mathbf{x}}(p(\mathbf{x}), q(\mathbf{x}))\)
\(q(\mathbf{x})=p\left(\mathbf{y}=f_{\mathbf{y}}(\mathbf{x})\right) p\left(\mathbf{z}=f_{\mathbf{z}}(\mathbf{x})\right) /\left|J_{\mathbf{x}}\right|\)。其中,\(J_{\mathbf{x}}=\operatorname{det}\left(\left.\frac{\partial g(\mathbf{y}, \mathbf{z} ; \theta)}{\partial[\mathbf{y}, \mathbf{z}]}\right|_{f_{\mathbf{y}}(\mathbf{x}), f_{\mathbf{z}}(\mathbf{x})}\right)=\left[\operatorname{det}\left(\frac{\partial f( \mathbf{x} ; \theta)}{\partial\mathbf x}\right)\right]^{-1}\)
作者也证明了,当\(\mathcal{L_y}\)、\(\mathcal{L_z}\)收敛到0的时候,\(\mathcal{L_x}\)也能保证是0。因此\(\mathcal{L_x}\)不改变最优解,但是在实践中提高了收敛效率。
最后,如果在网络的任何一端使用零填充,则需要损失项来确保没有信息被编码到附加的维度中。a)使用平方损失来保证这些值接近于零,b)在额外的逆训练过程中,用相同振幅的噪声覆盖那些填充维数,并最小化重构损失,这迫使这些维数被忽略。
最大均值差异(Maximum Mean Discrepancy,MMD)
这里作者讲的很粗略,我想起以前上深度学习课的时候讲过,这里拿出来复习一下。
MMD (最大均值差异) 是迁移学习, 尤其是Domain adaptation (域适应) 中使用最广泛 (目前) 的一种损失函数, 主要用来度量两个不同但相关的分布的距离。两个分布的距离定义为: \[ M M D(X, Y)=\left\|\frac{1}{n} \sum_{i=1}^{n} \phi\left(x_{i}\right)-\frac{1}{m} \sum_{j=1}^{m} \phi\left(y_{j}\right)\right\|_{H}^{2} \] 其中 H 表示这个距离是由 \(\phi()\) 将数据映射到再生希尔伯特空间(RKHS)中进行度量的。
MMD的关键在于如何找到一个合适的 \(\phi()\) 来作为一个映射函数。但是这个映射函数可能在不同的任务中都不是固定的, 并且这个映射可能高维空间中的映射, 所以是很难去选取或者定义的。那如果不能知道 \(\phi,\) 那MMD该如何求呢?我们先展 开把MMD展开: \[ M M D(X, Y)=\left\|\frac{1}{n^{2}} \sum_{i}^{n} \sum_{i^{\prime}}^{n} \phi\left(x_{i}\right) \phi\left(x_{i}^{\prime}\right)-\frac{2}{n m} \sum_{i}^{n} \sum_{j}^{m} \phi\left(x_{i}\right) \phi\left(y_{j}\right)+\frac{1}{m^{2}} \sum_{j}^{m} \sum_{j^{\prime}}^{m} \phi\left(y_{j}\right) \phi\left(y_{j}^{\prime}\right)\right\|_{H} \] 展开后就出现了 \(\phi\left(x_{i}\right) \phi\left(x_{i}^{\prime}\right)\) 的形式, 这样联系SVM中的核函数 \(k(*),\) 就可以跳过计算 \(\phi\) 的部分, 直接求 \(k\left(x_{i}\right) k\left(x_{i}^{\prime}\right)_{\circ}\) 所 以MMD又可以表示为: \[ M M D(X, Y)=\left\|\frac{1}{n^{2}} \sum_{i}^{n} \sum_{i^{\prime}}^{n} k\left(x_{i}, x_{i}^{\prime}\right)-\frac{2}{n m} \sum_{i}^{n} \sum_{j}^{m} k\left(x_{i}, y_{j}\right)+\frac{1}{m^{2}} \sum_{j}^{m} \sum_{j^{\prime}}^{m} k\left(y_{j}, y_{j}^{\prime}\right)\right\|_{H} \]
在高维问题中,特别是在基于GAN的图像生成中,可训练的Discriminator loss通常是首选的。但是MMD的效果也很好,并且更容易使用、代价更小,从而使训练更稳定。这种方法需要定义一个核函数,这里使用了一个逆多二次函数(inverse multiquadric)作为核函数:\(k\left(\mathbf{x}, \mathbf{x}^{\prime}\right)=1 /\left(1+\left\|\left(\mathbf{x}-\mathbf{x}^{\prime}\right) / h\right\|_{2}^{2}\right)\)
实验结果
人为构造的数据
作者构造了一个由8个单高斯分布组成的高斯混合分布\(p(\mathbf x)\)。前向过程是“样本-->标签”的过程,定义的过程也很简单,就是属于8个单高斯分布峰值的的样 本给打上对应的label。共有四种label:红色、蓝色、绿色、紫色

而逆向过程就是给定一种颜色,求该颜色的分布。
作者使用了不同种方法来实现逆向过程,从而进行对比:
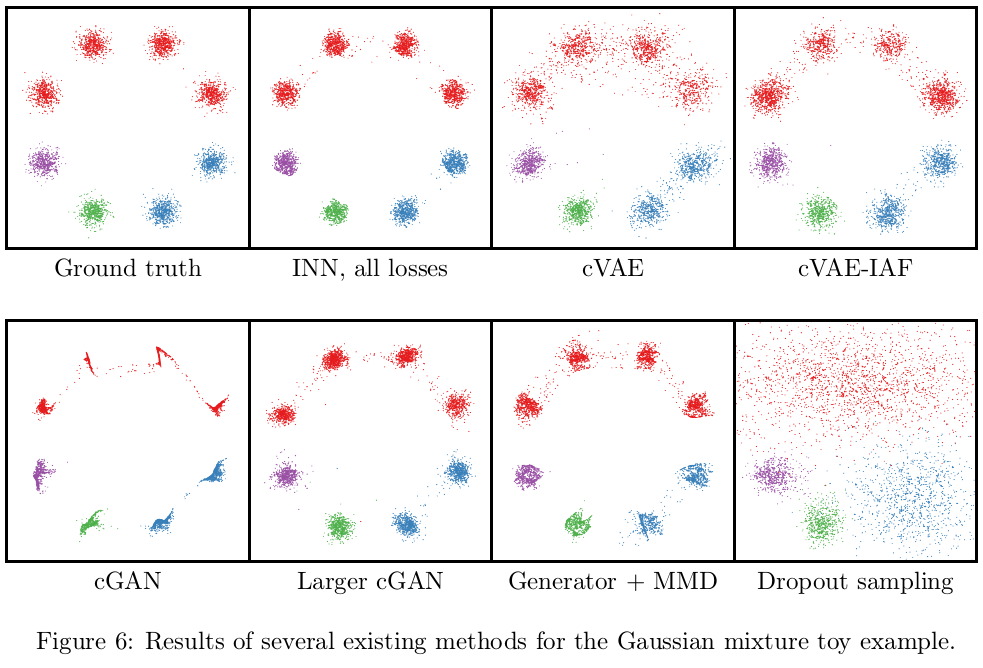
- cGAN:和INN模型大小差不多的条件GAN,参数量为10K,输入Generator的噪声向量的维度仅为2
- Larger cGAN:更大模型的条件GAN,参数量为2M,输入Generator的噪声向量的维度增加到128
- Generator+MMD:把条件GAN中的Generator保留,而把Discriminator换成MMD的判别方式(即把Generator的输出y与喂给Generator的x连接起来,与ground-truth的<x,y>在batch层面进行对比)。在这里作者发现:人工设置的核函数的MMD损失,效果居然好于Discriminator
- cVAE(-IAF):使用条件变分自编码器(加IAF)
- Dropout sampling:直接使用普通网络+dropout,拟合“颜色-->分布”这一逆过程
另外,作者对三个loss也做了消融实验:
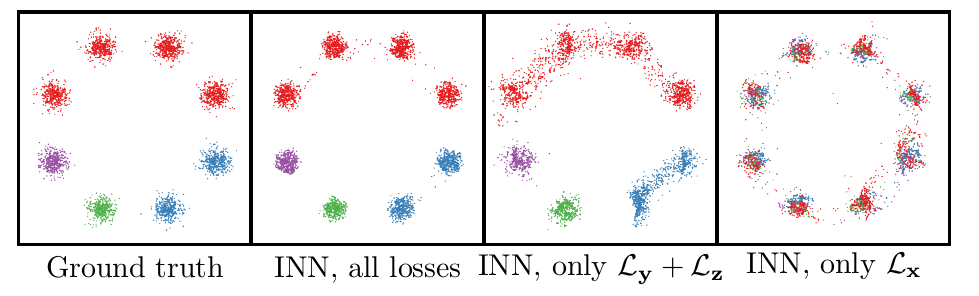
可以看到如果只使用正向的loss,则不能很好的拟合逆过程。相反地,只使用逆过程的loss(只是Lx)学习了正确的x分布,但丢失了所有的条件信息(颜色)。
我的思考
可逆神经网络(INN,Invertible Neural Networks)的核心目标是解决“逆向问题”,而这个逆向问题往往是ill-posed,也就是一个观测值可能有多个对应的系统参数。这样就需要建立一个”测量值-->系统参数的分布“的映射,引入隐变量\(\mathbf z\)这一随机变量保证了“单值-->概率分布”的映射。
根据我的查阅,类似的相关工作还有cGAN、cVAE、Normalizing Flow等,我将其思想进行以下的简要对比:
cGAN是直接利用了GAN可以学分布的特点,加入条件信息进行逆过程的学习,但是对正向过程没有显式的学习。同一般的GAN一样,Discriminator还是扮演了辨别分布真实性的角色。但根据本文的实验的结果,要达到和INN同样的效果,GAN需要更大的网络。
而在cVAE中,decoder完成了y-->x的逆过程(x=g(z;y)),但对于前向过程(x-->y),Encoder并没有显式地学习(这和cGAN很像,y都是只作为条件信息)。本文作者发现在逆任务中,cVAE表现比cGAN好,所以作为baseline。
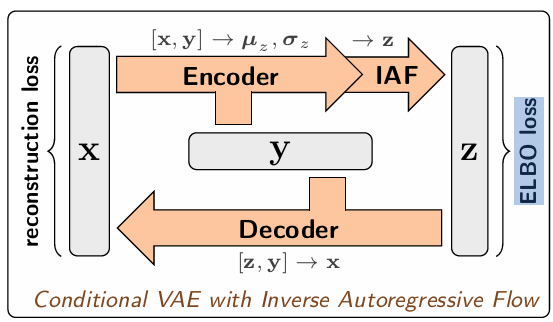
Normalizing Flow也使用了可逆的网络结构,但是其的主要关注点在于是否能高效的显式计算雅克比行列式,从而直接最大化似然概率。而本文INN虽然也是用的可逆的网络结构,但并没有使直接计算雅克比行列式,而是进行直接的逆向传播来采样,进而利用MMD,通过分布的样本来衡量分布之间的差异。而对于Normalizing Flow的确点,在网上看到一种说法,其使用简单的最大似然并没有覆盖拟合输入空间分布,而只是要求训练点的似然概率最大。所以我猜想本文没有使用Flow的思想,转而使用MMD去衡量分布差异,或许解决了这个问题。(本文实验没有与Normalizing Flow对比,实践存疑)
本文相当于借鉴了Normalizing Flow网络结构,但又不使用其直接最大化后验概率的思想,转而直接让样本数据在网络中来回跑,在两头用MMD加约束,感觉颇有Cycle-GAN的思想。不使用Discriminator而使用MMD,增加了训练的稳定性。
在超分辨领域,前向问题就是“HR退化为LR”,而逆问题即为超分过程,而正好也是ill-posed。上个月我读的一篇ECCV 2020的Learning the Super-Resolution Space with Normalizing Flow用的是Normalizing Flow的思想,学习“LR-->HR的分布“,基本也是这种问题抽象方式。因此,将其改成本文的INN应该也是可行的。这样就和invertible image rescaling的想法基本一致了。但是依据超分辨问题的特点,具体网络结构应该还有很多的改进空间(比如invertible image rescaling中的wavelet模块之类的)