论文背景
motivation
针对某个退化模型训练的SR网络,如果换了退化模型,性能就会有很大下降(比方说训练集用双三次下采样构造,而测试时遇到其他的退化模型)。于是作者从广义采样中受到了启发,出了一种改进现有的CNN框架的方法,即使用一个校正滤波器,能把一张LR图像变化到其他核模糊下的LR图像(如双三次核),进而提高test时SR网络的性能,具体分为非盲SR和盲SR两种情况:
- 在非盲SR中,LR图像的模糊核是已知的(但不一定和训练集的核匹配),于是作者构造的滤波器,可以提供一个将其转换到指定退化核LR图像的校正滤波器,并且是闭合解。
- 而在盲SR中,LR图像的模糊核是未知的,作者提出了一种能估计这张LR所需校正滤波器的算法。
相关知识
我查阅了相关文献,大致了解到广义采样的概念:
所谓广义采样是相对于经典的Nyquist-Shannon采样理论的。
Nyquist-Shannon采样
传统的Shannon采样是一种针对带限信号的等距理想采样,其处理过程如图所示。
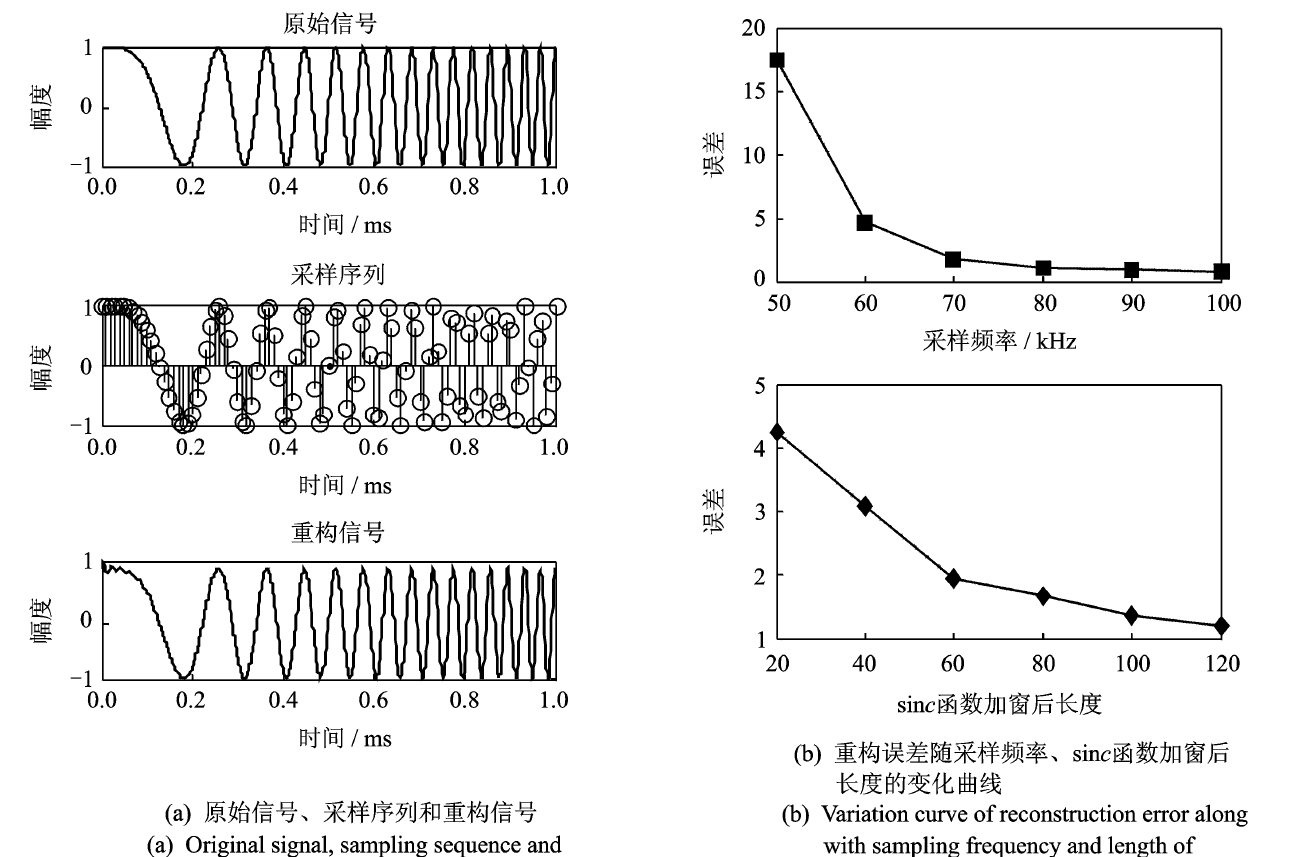
输入的连续信号\(x(t)\)经过前置滤波器变为带限信号,以Nyquist采样率进行采样获得离散信号: \[ \tilde{x}(t)=x(t) \cdot \delta(t)=\sum_{n \in \mathbf{Z}} x(n T) \delta(t-n T) \] 为了便于前置滤波器的实现,降低带外无用信号频谱重叠的影响,实际上信号的采样频率往往要比Nyquist采样率高。而信号重构可通过理想低通滤波器来实现,在时域等同于采用无限长的非因果冲激响应,即sinc函数插值重构得到: \[ \hat{x}(t)=\sum_{n \in \mathbf{Z}} x(n T) \sin c(t / T-n) \] 物理上重构的实现只能通过非理想的低通滤波或时域上现在与过去时刻的采样值通过内插来实现,但无论是非理想的低通滤波或有限长度的插值均会产生重构误差。以线性调频信号为例,通过仿真说明采样与重构的关系。假设原始信号的脉宽为1 ms,带宽为30 kHz。采样频率取70 kHz,具体仿真结果见下图。
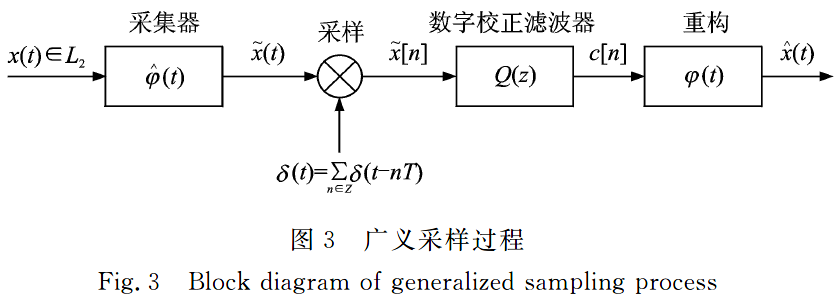
可以看出,当采样频率为70kHz时基本上能够无失真地恢复原始信号,有重构误差是因为在Matlab中Sinc函数取值必须进行截断,对应频谱是非理想低通滤波器,从而造成误差。由图2(b).上图可知,重构误差随采样频率的增大而减小,当采样频率低于Nyquist 采样率(60 kHz)时,重构误差将迅速上升。图2(b)下图则表示重构误差随Sinc函数加窗截断后长度的增加而减小,当点数取无限长时理论误差为零。因此,Shannon采样的重构精度同时受采样频率与插值内核的长度影响,而工程实现上不可能采用过高的采样频率与过长的插值长度,这正是Shannon采样局限性的体现。
广义采样
由式(5)可以发现,\(\{\sin c(t-n), n \in Z\}\)其实是一个线性无关且相互正交的函数族。即sinc函数在时间轴上的平移函数族构成了所有带限函数组成的函数空间的一组正交基。这里定义一个基本近似空间\(V\)即 \[ V(\varphi)=\left\{s(x)=\sum_{k \in \mathbf{Z}} c(k) \varphi(x-k): c \in l_{2}\right\} \] 表示空间V内任意的连续函数s(x)都能够表示为系数c(k)的序列。
信号的采样及重构,实际上就是对给定的信号,通过选取合适的基,使信号在这组基下的投影具有所需要的性质。如果在某个基下不符合要求,那么就将其变换到另一个基下表示。与Shannon采样对应,这里给出广义采样的处理框架如图所示:
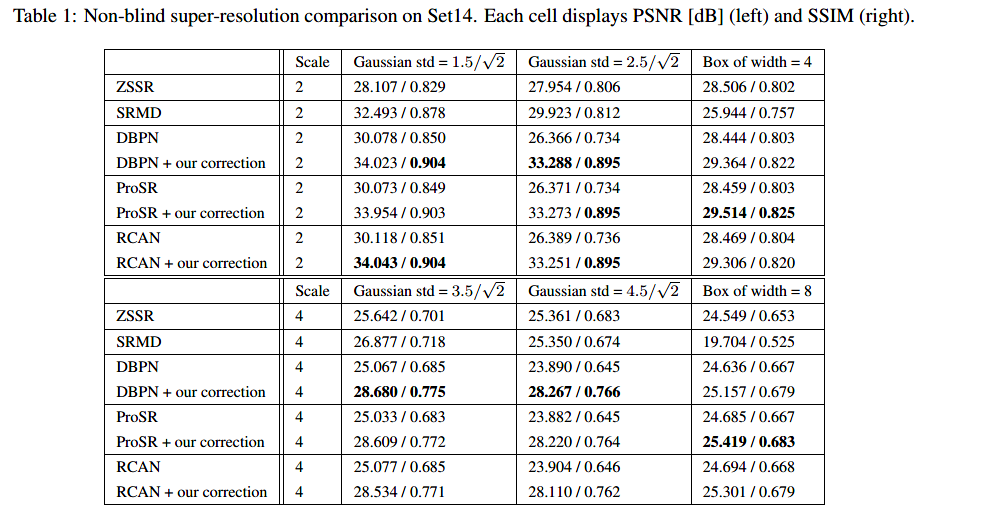
将连续信号与基函数求内积、采样并经过一个数字校正滤波器(校正滤波器的作用是将与采样核相关联的采样系数,变换为与重构核相匹配的系数),得到其在该基底上的离散展开系数,再由广义上的重构公式即可恢复原始信号。
广义采样理论提供了一种框架和条件,在这种框架和条件下,在一定的基采样后的信号可以在不同的基上重建。
方法详述
对于退化过程,\(\mathbf{x} \in \mathbb{R}^{n}\),\(\mathbf{y} \in \mathbb{R}^{m}\),\(n>m\): \[ \mathbf{y}=(\mathbf{x} * \mathbf{k}) \downarrow_\alpha \] 作者写成一个线性变换的形式: \[ \mathbf{y}=\mathcal{S}^{*} \mathbf{x} \] 其中,\(\mathcal{S}^{*}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\)。即把模糊+下采样整合在一起,即\(\mathcal{S}^{*}\)对应了真实的下采样核的退化过程:
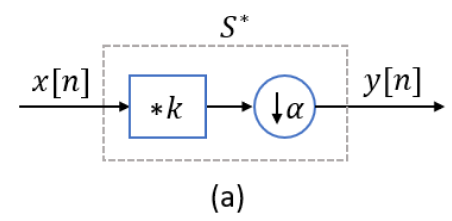
令\(\mathcal{R}^{*}\)为双三次下采样退化过程对应的线性变换,即\(\mathbf{y}_{b i c u b}=\mathcal{R}^{*} \mathbf{x}\)。
非盲SR时的闭合解
定义\(\mathcal{S}\)与\(\mathcal{R}\)分别为为\(\mathcal{S}^{*}\)与\(\mathcal{R}^{*}\)的伴随算子。作者假设\(\mathbf{x}\)能从\(\mathcal{R}^{*} \mathbf{x}\)使用算子\(\mathcal{R}\left(\mathcal{R}^{*} \mathcal{R}\right)^{-1}\)恢复: \[ \mathbf{x}=\mathcal{R}\left(\mathcal{R}^{*} \mathcal{R}\right)^{-1} \mathcal{R}^{*} \mathbf{x} \] 即利用了\(\mathcal{R}^{*}\)的伪逆,可从从\(\mathbf{y}_{\text {bicub}}=\mathcal{R}^{*} \mathbf{x}\)恢复出原HR图像。
然后作者表示,对于不是双三次退化的LR图像\(\mathbf y\),可以引入一个估计过程: \[ \hat{\mathbf{x}}=\mathcal{R} \mathcal{H} \mathbf{y} \] 即先对\(\mathbf y\)作一个变换\(\mathcal H\),在经过原始的超分辨过程\(\mathcal R\)。
作者证明了\(\mathcal{H}=\left(\mathcal{S}^{*} \mathcal{R}\right)^{-1}: \mathbb{R}^{m} \rightarrow \mathbb{R}^{m}\),(前提是\(\operatorname{null}\left(\mathcal{S}^{*}\right) \cap \operatorname{range}(\mathcal{R})=\{0\}\)): \[ \begin{aligned} \hat{\mathbf{x}} &=\mathcal{R} \mathcal{H} \mathbf{y} \\ &=\mathcal{R} \mathcal{H} \mathcal{S}^{*} \mathbf{x} \\ &=\mathcal{R} \mathcal{H} \mathcal{S}^{*} \mathcal{R}\left(\mathcal{R}^{*} \mathcal{R}\right)^{-1} \mathcal{R}^{*} \mathbf{x} \end{aligned}\\ \begin{aligned} \hat{\mathbf{x}} &=\mathcal{R}\left(\mathcal{S}^{*} \mathcal{R}\right)^{-1} \mathcal{S}^{*} \mathcal{R}\left(\mathcal{R}^{*} \mathcal{R}\right)^{-1} \mathcal{R}^{*} \mathbf{x} \\ &=\mathcal{R}\left(\mathcal{R}^{*} \mathcal{R}\right)^{-1} \mathcal{R}^{*} \mathbf{x}=\mathbf{x} \end{aligned} \]
据此,作者给出校正滤波器的初始版本\(\mathbf h_0\): \[ \mathbf{h}_{0}=\operatorname{IDFT}\left\{\frac{1}{\operatorname{DFT}\left\{\left(\mathbf{k} * \operatorname{flip}\left(\mathbf{k}_{\text {bicub}}\right)\right) \downarrow_{\alpha}\right\}}\right\} \] 但是对于\(\hat{\mathbf{x}}=\mathcal{R} \mathcal{H} \mathbf{y}\)这个估计过程,是没有用到任何的自然图像的先验的。而对于一个使用双三次下采样的数据集训练好的CNN网络\(f\),估计过程可以写为\(\hat{\mathbf{x}}=f(\mathbf{h} * \mathbf{y})\)。\(f\)学到了\(\mathcal{R}\left(\mathcal{R}^{*} \mathcal{R}\right)^{-1}\)这一$^{} \(的反过程作为先验。所以在网络\)f\(中,他其实隐含的完成了\)(^{} ){-1}\(的过程,于是在对\)y\(进行滤波的时候,先要加上\){*} $的过程,即: \[ \begin{aligned} \mathbf{h} &=\operatorname{IDFT}\left\{\frac{\operatorname{DFT}\left\{\left(\mathbf{k}_{\text {bicub}} * \operatorname{flip}\left(\mathbf{k}_{\text {bicub}}\right)\right) \downarrow_{\alpha}\right\}}{\operatorname{DFT}\left\{\left(\mathbf{k} * \operatorname{flip}\left(\mathbf{k}_{\text {bicub}}\right)\right) \downarrow_{\alpha}\right\}}\right\} \\ & \triangleq \operatorname{IDFT}\left\{\frac{F_{\text {numer}}}{F_{\text {denom}}}\right\} \end{aligned} \] 作者表示,为了数值稳定性,式子改成了这样: \[ \mathbf{h}=\operatorname{IDFT}\left\{F_{n u m e r} \cdot \frac{F_{\text {denom}}^{*}}{\left|F_{\text {denom}}\right|^{2}+\epsilon}\right\} \]
盲SR的估计算法
对于盲SR,作者表示,任务变成了既要估计模糊核\(\mathbf k\)又要估计校正滤波器\(\mathbf h\)。作者提出了一个估计\(\mathbf k\)的目标函数: \[ \xi(\mathbf{k})=\left\|\mathbf{y}-\mathcal{S}^{*} f(\mathcal{H} \mathbf{y})\right\|_{\mathrm{Hub}}+\left\|\mathbf{m}_{\mathrm{cen}} \cdot \mathbf{k}\right\|_{1}+\|\mathbf{k}\|_{1} \] \(\left\|\ \right\|_{\mathrm{Hub}}\)表示Huber loss,\(\mathcal H\)就对应的(12)式中的滤波器,\(\mathbf{m}_{\mathrm{cen}}(x, y)=1-\mathrm{e}^{-\frac{\left(x^{2}+y^{2}\right)}{32 \alpha^{2}}}\)。最后两项是正则化因子:最后一项促进k的稀疏性,倒数第二项用于集中k的密度(?)。
具体求\(\mathbf k\)的过程,是把其作为一个线性CNN的参数去优化:\(\mathbf{k}=\mathbf{k}_{0} * \mathbf{k}_{1} * \mathbf{k}_{2} * \mathbf{k}_{3}\).
具体算法如下:

在每次迭代中,都得到了\(\mathbf k\)和校正滤波器\(\mathbf h\)的估计值。
实验结果
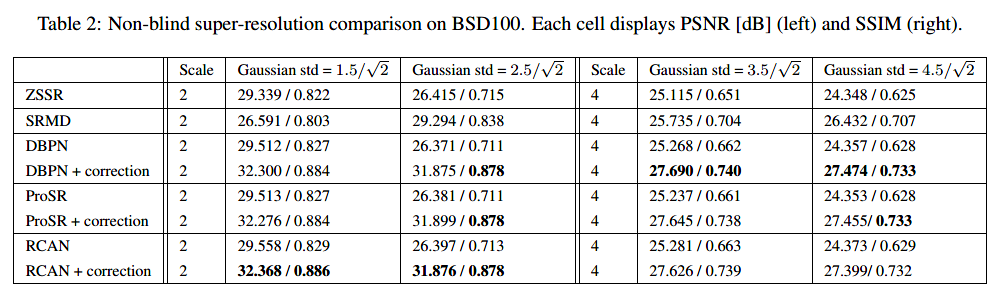
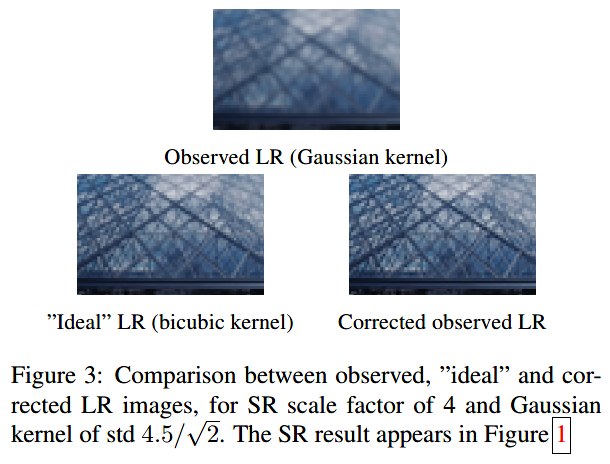
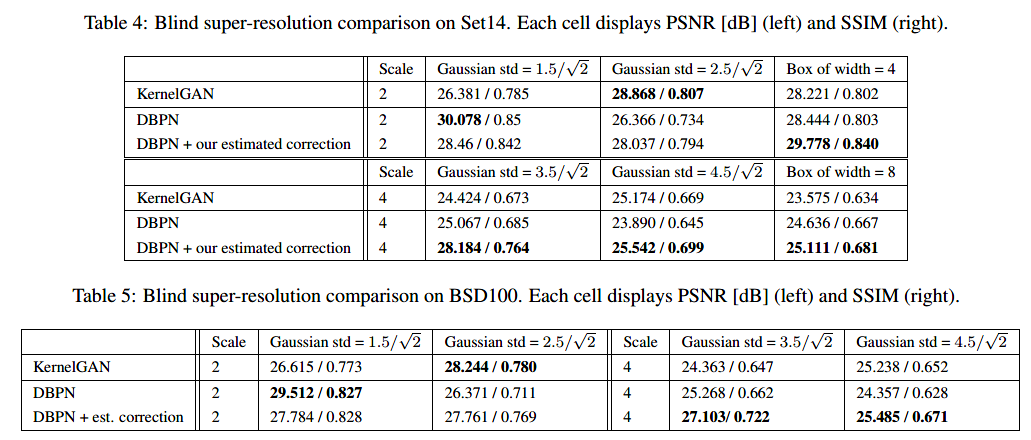
盲的过程:


总结与思考
校正滤波器就对应了广义采样中的数字校正滤波器;而不同的模糊核就视作了不同的采样基底。
从整体来看,把LR转换成“干净”退化模式(比如双三次)的思路,和以前看的利用GAN转换domain的想法类似,但是是从完全不同的角度。
本文把SR问题视作一种信号采样-恢复的过程,是我之前没见过的角度。而我之前没有学过信息论,对相关知识了解较少,花了大量时间去查阅相关资料与文献。以后应该把相关知识系统性的学一下。