参考了文章：
相机的内参和外参
相机内参
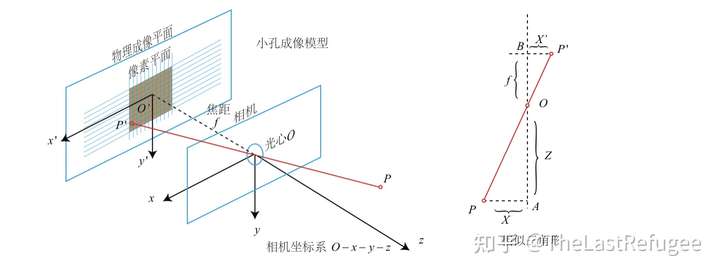
左图中，把相机看作是针孔，现实世界中的点P经过相机的光心O，投影到物理成像平面上，变为点P'。
右图中，对这个模型进行了一个简化，将其看作是一个相似三角形。
设\(O-x-y-z\)为相机坐标系，习惯上我们把z轴指向相机前方，x向右，y向下。O为摄像机的光心，也是针孔模型中的针孔。
设现实世界中的点的的坐标为\([X,Y,Z]^T\)，而成像点的坐标为\([X', Y',Z']\)，物理成像平面到光心的距离为\(f\)，也就是焦距。所以根据右图的相似三角形关系，有以下式子： \[ \frac{Z}{f}=-\frac{X}{X^{\prime}}=-\frac{Y}{Y^{\prime}} \] 其中，有负号是因为坐标轴方向，也就表示了成的像是倒立的。
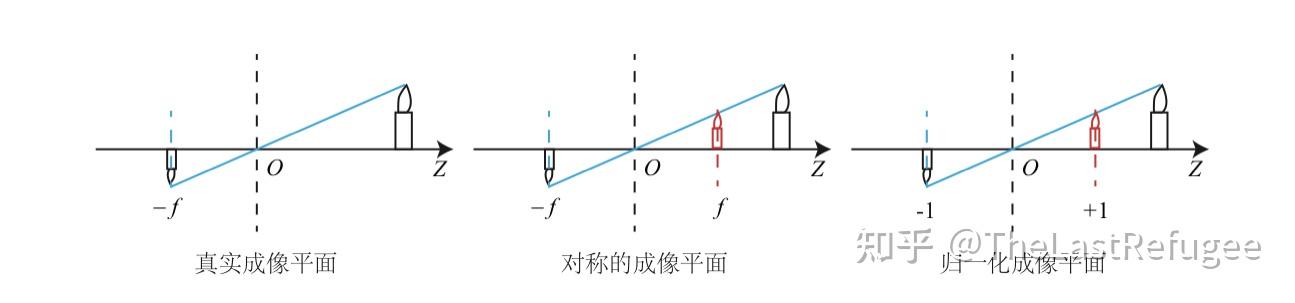
为了表示起来更方便，我们把成像平面从相机的后面对称到前面去，如下图所示。这样，负号就没有了。
\[
\frac{Z}{f}=\frac{X}{X^{\prime}}=\frac{Y}{Y^{\prime}}
\] 整理出P'的坐标： \[
\begin{aligned}
&X^{\prime}=f \frac{X}{Z} \\
&Y^{\prime}=f \frac{Y}{Z}
\end{aligned}
\] 然而物理成像平面是不够的，还需要放在像素坐标系里面。设P'在像素坐标系下对应的坐标为\([u,v]^T\)。
那么物理成像平面到像素坐标系的变换只涉及到缩放和平移。设像素坐标在u轴上缩放了\(\alpha\)倍，在v轴上缩放了\(\beta\)倍。同时原点平移了\([c_x, c_y]^T\)。那么可以得到P'与像素坐标的关系： \[ \begin{aligned} &u=\alpha X^{\prime}+c_{x} \\ &v=\beta Y^{\prime}+c_{y} \end{aligned} \] 代入P与P'的关系式可得： \[ \begin{aligned} &u=\alpha f \frac{X}{Z}+c_{x}=f_{x} \frac{X}{Z}+c_{x} \\ &v=\beta f \frac{Y}{Z}+c_{y}=f_{y} \frac{Y}{Z}+c_{y} \end{aligned} \] 用齐次坐标，把上式写出矩阵的形式： \[ \left(\begin{array}{l} u \\ v \\ 1 \end{array}\right)=\frac{1}{Z}\left(\begin{array}{ccc} f_{x} & 0 & c_{x} \\ 0 & f_{y} & c_{y} \\ 0 & 0 & 1 \end{array}\right)\left(\begin{array}{c} X \\ Y \\ Z \end{array}\right)=\frac{1}{Z} \mathbf{K} \mathbf{P} \] 也可以把Z写到等式左边去，就变成了： \[ Z\left(\begin{array}{l} u \\ v \\ 1 \end{array}\right)=\left(\begin{array}{ccc} f_{x} & 0 & c_{x} \\ 0 & f_{y} & c_{y} \\ 0 & 0 & 1 \end{array}\right)\left(\begin{array}{l} X \\ Y \\ Z \end{array}\right)=\mathbf{K} \mathbf{P} \] 上式中，\(\mathbf{K}\)即为相机的内参矩阵(Intrinsics)。通常来说，相机的内参在出厂之后就是固定的了。
相机外参
在上面的推导中，我们用的是\(P\)在相机坐标系的坐标（也就是以相机光心为O点）。应该先将世界坐标系的\(P_w\)转换为相机坐标系\(P\)。
这里需要用到相机的位姿，由旋转矩阵\(\mathbf R\)与平移向量\(\mathbf t\)来表示，故： \[ \mathbf{P}=\left(\begin{array}{ccc} X \\ Y \\ Z \end{array}\right)=\mathbf{R} \mathbf{P}_{\mathbf{w}}+\mathbf{t} \] 写成齐次形式： \[ \mathbf P_{齐}=\left(\begin{array}{c} X \\ Y \\ Z \\ 1 \end{array}\right)=\left(\begin{array}{cc} \mathbf R & \mathbf t \\ 0^{3} & 1 \end{array}\right)\left(\begin{array}{c} x_{w} \\ y_{w} \\ z_{w} \\ 1 \end{array}\right) \] \(\left(\begin{array}{cc} \mathbf R & \mathbf t \\ 0^{3} & 1 \end{array}\right)\)即为外参矩阵(Extrinsics)
相机畸变矫正
相机主要包括径向畸变和切向畸变
径向畸变
径向畸变（枕形、桶形）：光线在远离透镜中心的地方比靠近中心的地方更加弯曲，如下图
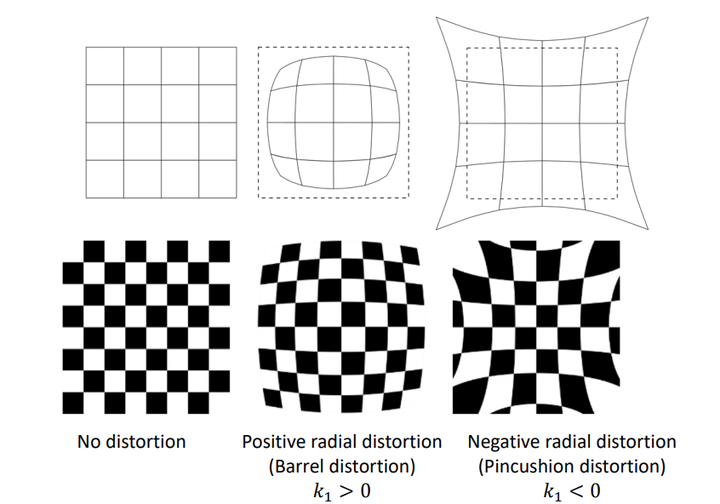
有径向畸变的原始图像和矫正后的图像:
\(\mathrm{r}\) 是以图像 \(\left[u_{0}, v_{0}\right]\) 中心为半径的圆 \[ r^{2}=\left(u-u_{0}\right)^{2}+\left(v-v_{0}\right)^{2} \] 根据图像的畸变的程度, 有的时候为了简化相机模型, 高阶项 \(k_{2}, k_{3}\) 有时候会被舍弃。
切向畸变
切向畸变：透镜不完全平行于图像平面，即sensor装配时与镜头间的角度不准，这样会导致图像的中心有所偏移(decentering)，如下图
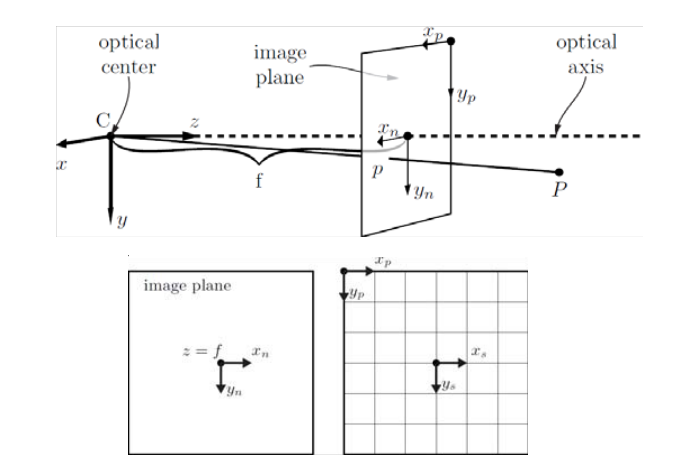
上述式子中加入切向畸变后： \[ \left[\begin{array}{l} u_{d} \\ v_{d} \end{array}\right]=\left(1+k_{1} r^{2}+k_{2} r^{4}+k_{3} r^{6}\right)\left[\begin{array}{l} u-u_{0} \\ v-v_{0} \end{array}\right]+\left[\begin{array}{l} 2 k_{4}\left(u-u_{0}\right)\left(v-v_{0}\right)+k_{5}\left(r^{2}+2\left(u-u_{0}\right)^{2}\right) \\ k_{4}\left(r^{2}+2\left(v-v_{0}\right)^{2}\right)+2 k_{5}\left(u-u_{0}\right)\left(v-v_{0}\right) \end{array}\right]+\left[\begin{array}{l} u_{0} \\ v_{0} \end{array}\right] \]