论文背景
对于一般的盲超分方法,一般都分为两步:
- 从LR图像中估计一个模糊核
- 基于估计的模糊核,估计SR图像
- 这两步通常是使用两个不同的模型(各自独立训练出来的)。而第一步的微小误差会给第二步的超分结果造成很大的损失。
- 第一步只是通过LR中的信息去估计模糊核,信息来源比较有限,模糊核估计的不准
因此,虽然这两个模型各自都能表现良好,但当它们组合在一起时,最终结果可能不是最优的。作者的思路是用一个交替迭代的优化算法。Restorer基于给定的模糊核,把LR图像超分辨为SR图像;而Estimator从LR、SR中估计模糊核,如此循环往复即可迭代。然后把这个网络展开,形成一个端到端的可训练的网络,作者称为DAN(Deep Alternating Network)。
这样,从LR和SR中,估计模糊核更合理一些。更重要的是,在展开网络之后,相当于Restorer是使用Estimator生成的核做训练,而不是ground-truth的核。所以Restorer更能容忍Estimator的估计误差。
方法详述
问题抽象
盲超分的过程可以形式化为: \[ \underset{\mathbf{k}, \mathbf{x}}{\arg \min }\left\|\mathbf{y}-(\mathbf{x} \otimes \mathbf{k}) \downarrow_{s}\right\|_{1}+\phi(\mathbf{x}) \]
而对于以往的“两步”盲超分,其实质上是解以下优化过程: \[ \left\{\begin{array}{l} \mathbf{k}=M(\mathbf{y}) \\ \mathbf{x}=\underset{\mathbf{x}}{\arg \min }\left\|\mathbf{y}-(\mathbf{x} \otimes \mathbf{k}) \downarrow_{s}\right\|_{1}+\phi(\mathbf{x}) \end{array}\right. \] 而本文的迭代过程,其实为: \[ \left\{\begin{array}{l} \mathbf{k}_{i+1}=\underset{\mathbf{k}}{\arg \min }\left\|\mathbf{y}-\left(\mathbf{x}_{i} \otimes \mathbf{k}\right) \downarrow_{s}\right\|_{1} \\ \mathbf{x}_{i+1}=\underset{\mathbf{x}}{\arg \min }\left\|\mathbf{y}-\left(\mathbf{x} \otimes \mathbf{k}_{i}\right) \downarrow_{s}\right\|_{1}+\phi(\mathbf{x}) \end{array}\right. \] 第一行为Estimator的过程,第二行为Restorer的过程。其实对于Estimator过程,k是存在解析解的,但是作者发现,解析解的计算更费时,而且微小的噪声将很大程度上影响其鲁棒性。
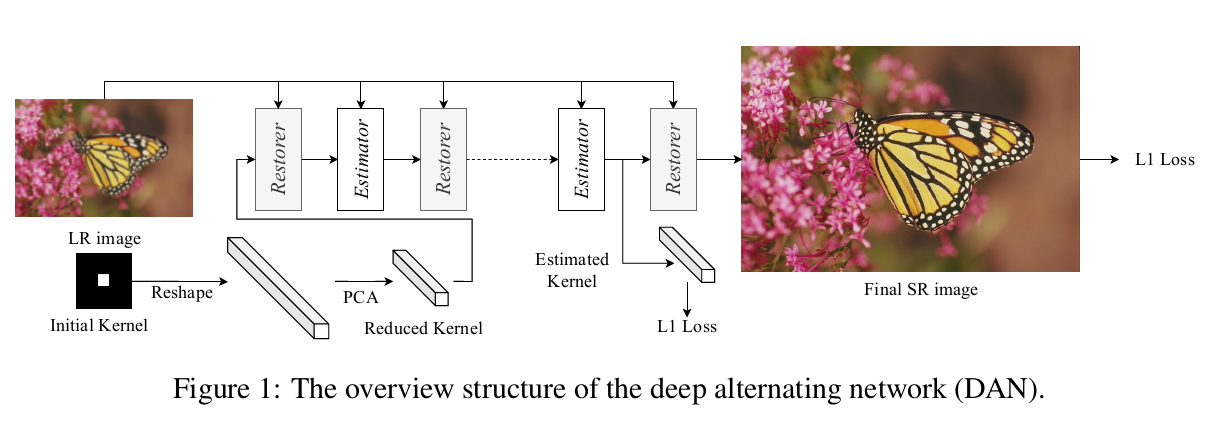
如图所示,先把模糊核k初始化为一个中心为1,其他都为0的狄拉克函数。然后将其重新排列为一个向量,接着使用PCA进行降维,输入到网络中。由于两个模块的参数在不同的迭代之间(迭代次数为4)是共享的,因此整个网络可以很好地训练,对中间结果没有任何限制。
比较特别的是,当scale=1时,SAN就变成了一个去噪网络。
网络结构
Estimator的输入是LR+SR,Restorer的输入是LR+k。所以把LR看成基础输入,而SR或者模糊核看成条件输入。在迭代的时候,基础输入LR保持不变,而条件输入交替迭代更新。
为了保证Estimator和Restorer的输出都和其条件输出相关,作者提出了一个条件残差块(CRB),应用于Estimator和Restorer中:
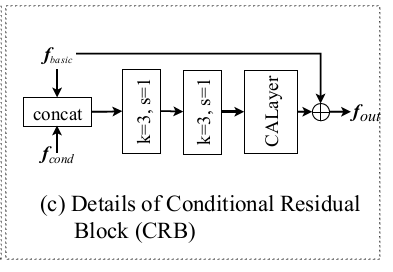
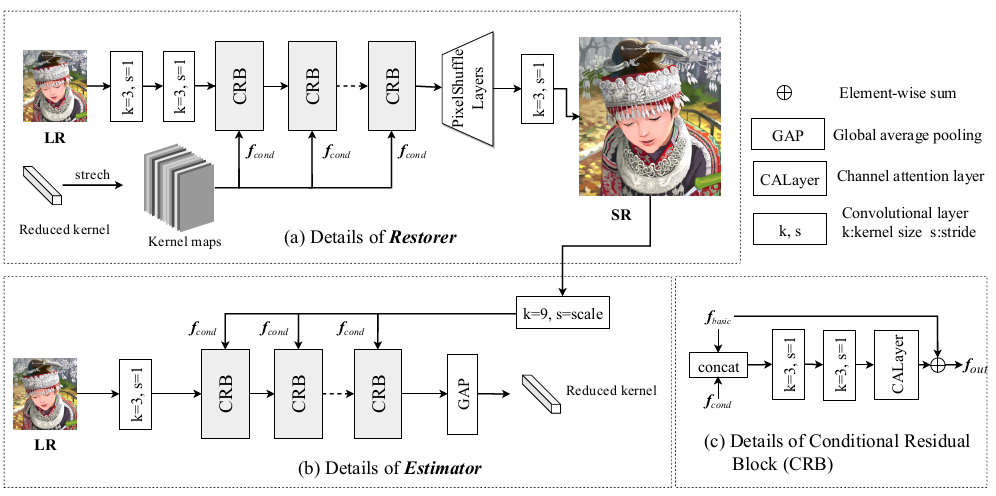
形式化表述为: \[ f_{\text {out}}=R\left(\text {Concat}\left(\left[f_{\text {basic}}, f_{\text {cond}}\right]\right)\right)+f_{\text {basic}} \] 进而Estimator和Restorer的结构如图:
实验结果
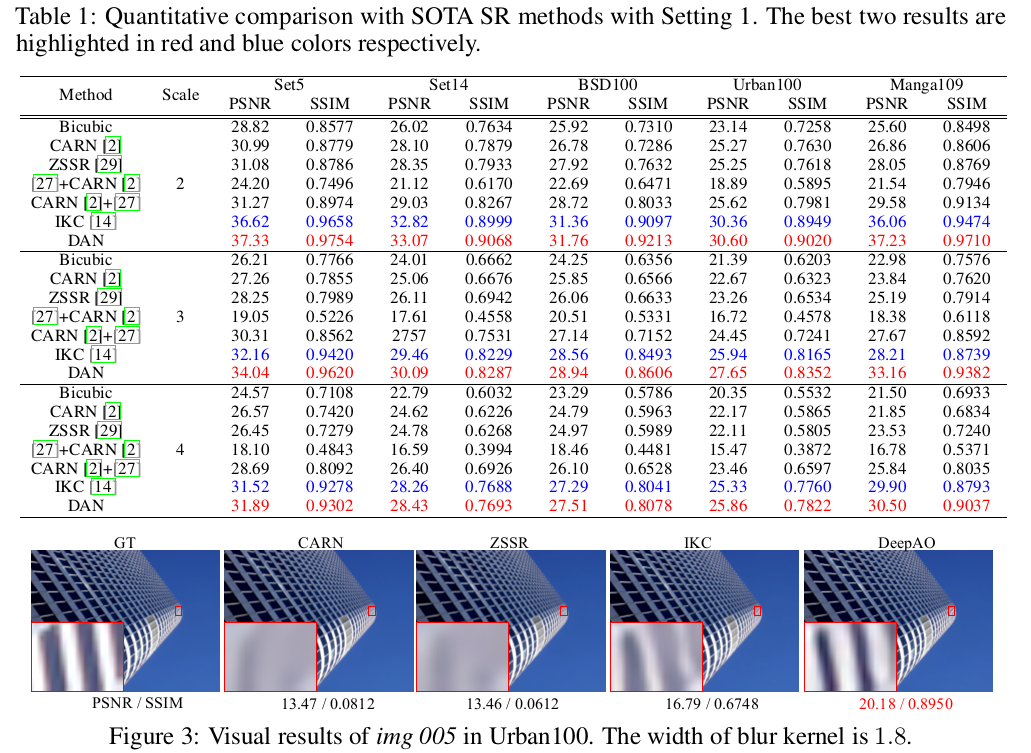


总结与思考
- 其实盲超分是一个“先有鸡还是先有蛋”的问题。一方面,需要知道模糊核,才能更好的把LR转换为HR(即已知模糊核,非盲超分);而另一方面,要知道模糊核,则最好需要HR与对应的LR图像(只通过LR估计模糊核其实是信息不够的)。于是作者提出把这个“鸡生蛋、蛋生鸡”的问题一直迭代下去
(鸡生蛋生鸡生蛋生鸡生蛋……这样最后得到了更好的鸡和更好的蛋),把整个迭代过程展开为网络,从而端到端地训练。 - 这篇文章乍一看和CVPR 2019的同为迭代方法的IKC很像,但是仔细分析也有很多的不同:
- IKC分为三个模型,SFTMD模型用于k+LR-->HR,Predictor用于LR-->k,Corrector用于HR+k-->∆k。训练过程中,SFTMD单独训练,而Predictor与Corrector迭代训练。正向推理过程中,Predictor只在最开始用到,而之后交替使用SFTMD与Corrector迭代。
- 而本文只有两个模型,Restorer用于k+LR-->HR,Estimator用于HR+LR-->k,二者可以互相迭代。之所以少一个Predictor模型,是因为作者将k直接初始化为一个δ核。
- IKC的训练不是端到端的,而是在每个迭代中,都使用一次反向传播算法去更新参数;而本文的网络框架本质上和RNN的模型很像,训练过程是端到端的,只不过传播过程是循环的(即模型参数是共享的)。
- 观察这两个工作,本质上SFTMD ≈ Restorer,而Predictor+Corrector≈Estimator (前者为IKC中的模块,后者为本文的模块)。从本篇文章的描述,对于Estimator来说,LR是basic input,HR是conditional input。如此倒过头来看IKC,似乎把Estimator拆分成只推理一次的Predictor和不断矫正的Corrector是有一定道理的(LR作为basic input只需输入一次,而HR作为不断变化的conditional input需要不断迭代矫正)。
- IKC的训练过程,每次迭代都是要使Corrector尽可能将k矫正到ground-truth。而本文的端到端的训练过程,每一次迭代并不一定要使Estimator估计出ground-truth,而最终能估计出ground-truth即可。