这篇算是一篇超分辨/去噪的数据增强方面的文章,与以往的数据增强不同的是,它是在频域的角度设置了数据增强方法。
论文背景
作者指出,基于学习的超分辨/去噪的CNN网络,总是基于一个庞大的数据集来训练。而这个数据集往往是通过把ground-truth图片经过一个模糊核/有限的模糊核集合进行退化构造出LR图片。但是在测试过程中,往往需要针对一个未知模糊核的LR图像来进行SR,或是对一个未知等级的噪声进行denoising。作者指出,现有的SR模型都对有限的退化模型产生了过拟合。作者在频域中分析了这一点。进一步地,作者更加形式化地揭示了SR过程中隐含的一种条件学习——“在已知低频的情况下学习高频”。据此,作者提出了本文的主要工作——随机频率掩蔽(Stochastic Frequency Masking, SFM)。
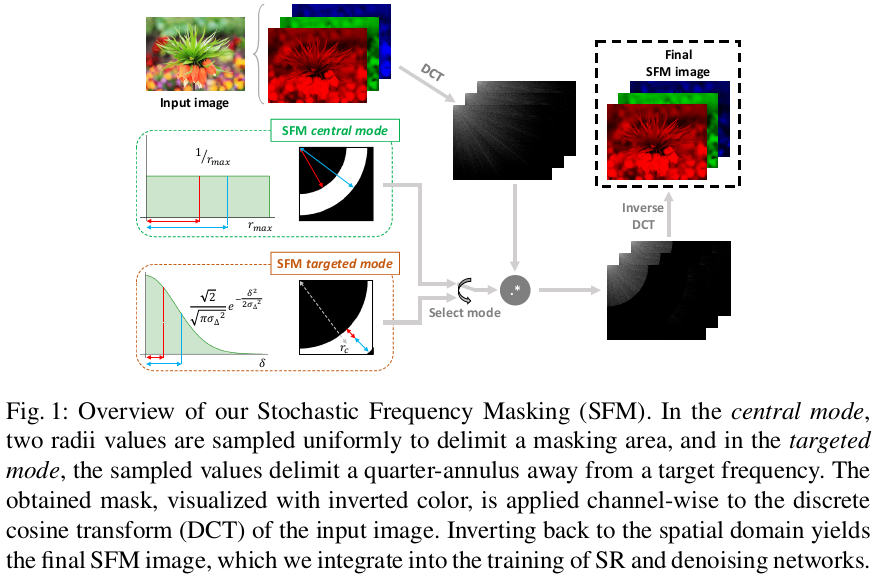
方法详述
背景知识
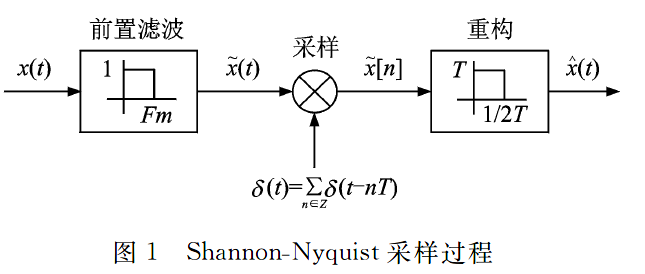
在信号与系统中学习过,一个离散的信号x(n),设它的DTFT(离散时间傅里叶变换)为X(ω),则对x(n)的采样间隔。为T的采样信号z的DTFT为\(Z(\omega)=\frac{1}{T} \sum_{k=0}^{T-1} X((\omega+2 \pi k) / T)\)。这T个X(ω)的副本会使得Z(ω)频谱的高频部分发生混叠。即如果想要从z恢复到x时,高频的混叠就会造成视觉扭曲。因此有时也在下采样的过程中使用一个(非理想的)低通滤波器,先把可能重叠的高频部分减弱,这个低通滤波器就对应了模糊核。
这里我对这个逻辑还是有疑问,为什么是为了防止混叠才用这个模糊核。难道模糊核不是退化模型中客观存在的过程吗?
原文如下:
真实的模糊核毕竟只是所有数学上所有可能的核的一个子空间。但是,在以前的工作中,这个子空间并没有很好的定义,而总是定义为一个空域的卷积核,比如一个高斯核,即试图模拟原始捕获设备的点扩展函数(可以理解为冲激响应函数)。但是实际上,即使是单个成像设备也会产生多个模糊核,甚至不一定是高斯核。
SR过程在频域上的可视化实验
作者做了一个实验,先使用\(\sigma=4.1\)的高斯核构造一个训练数据集,去训练一个RRDB网络。然后在测试过程,利用这个网络来SR一个由\(\sigma=7.4\)的高斯核构造的LR图像。
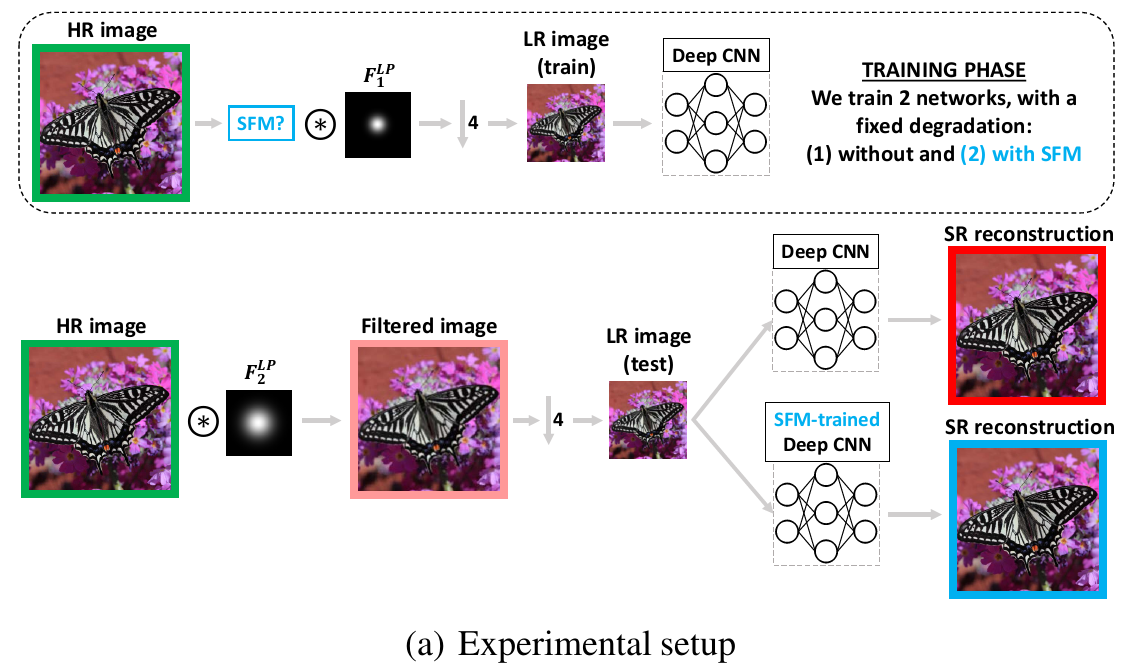
对于测试过程,在频域分别分析了groud-truth、LR、SR图片的功率谱密度:
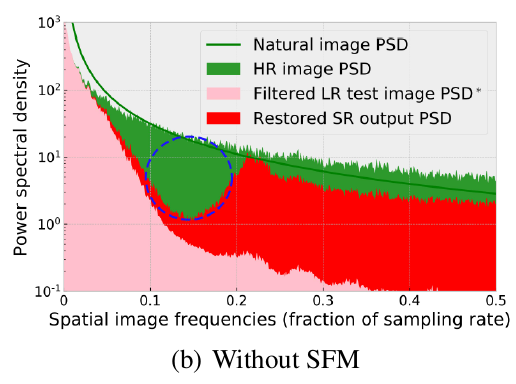
对于一张自然图像,功率谱密度一般满足\(1/f^\alpha\)的幂函数(绿色)
而退化后的LR图像,会缺少大量的高频信息(粉色)
而经过SR网络后,SR图像的部分高频强度会被恢复(红色)
- 但是,从图中可以看出,恢复的主要是频率大于\(0.2\pi\)的高频信息。也就是构造训练集时,原始的HR图像中被高斯低通滤波器滤掉的那一部分。
- 而构造测试集时,其实使用的是一个更加“严格的”低通滤波器(空域上高斯核的\(\sigma\)与频域上高斯滤波器的\(\sigma\)是负相关的,\(g(x)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-\frac{x^{2}}{2 \sigma^{2}}}\) <->\(G(f)=e^{-\frac{f^{2}}{2 / \sigma^{2}}}\)),所以它的最低截止频率比训练集中的低。
- 这导致了在恢复的SR输出中没有得到的缺失频率分量(上图中的蓝色虚线圆)
而作者表示,用了他提出的SFM就不会有这个问题:
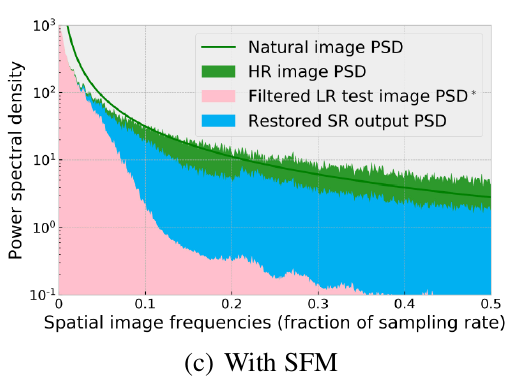
隐含的条件学习
如果抗混叠时使用的滤波器是一个理想低通滤波器(高频全去掉,低频不受影响),那么SR网络对应如下的条件学习: \[ P\left(I^{H R} \otimes F^{H P} \mid I^{H R} \otimes F^{L P}\right) \] 意为从低频信息中去学习高频信息。
而对于实际上的非理想低通滤波器,它既不能全部去掉高频,又不能完全不衰减低频。于是对应了如下的条件学习: \[ P\left(I^{H R} \otimes F^{H P} \mid I^{H R} \otimes F_{o}^{L P}\right), \quad P\left(I^{H R} \otimes F^{L P}-I^{H R} \otimes F_{0}^{L P} \mid I^{H R} \otimes F_{o}^{L P}\right) \]
把以上理论扩展到去噪
高斯白噪声的功率谱密度是一条水平线,噪声加在原始的图像上,形成了信噪比的变化。而每个频率上的信噪比,随着频率增加而降低(即\(1/f^\alpha\)曲线):
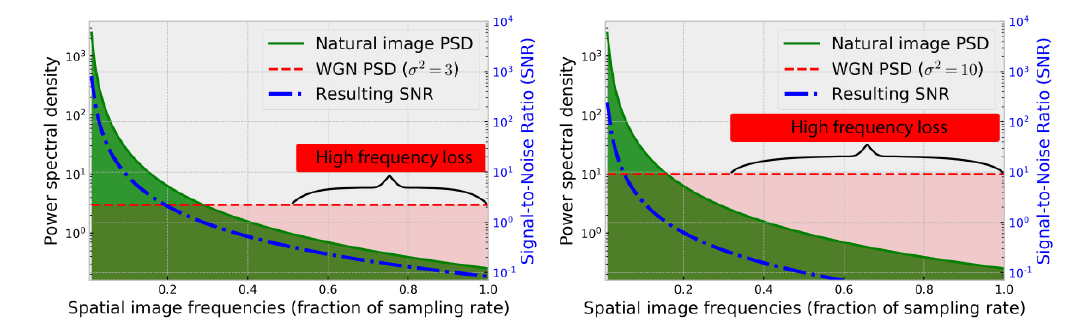
换句话说,高频几乎完全被噪声所取代,而低频受噪声的影响则小得多。并且,当噪声水平越高时,启动频率(超过这个频率,信噪比就非常小)越低。这和上述SR的分析是一致的。
综上,无论是SR还是denoising,都存在一种隐含条件学习,可以在低频部分受到较少影响的情况下,预测高频部分的损失。
随机频率掩蔽(SFM)
把图片使用离散余弦变换到频域上,然后在通道级别上进行频率掩蔽。频率掩蔽带都是一个四分之一的圆环,即只需确定掩蔽带的频率上下界即可。具体确定掩蔽带的方法有两种模式:中心模式、目标模式
中心模式
中心模式是指,掩蔽带的上下界都是\([0,r_M]\)的均匀分布,\(r_M\)是最大半径。于是根据概率论的知识很容易推出,给定一个频率\(r_\omega\),被掩蔽的概率是: \[ P\left(r_{I}<r_{\omega}<r_{O}\right)=2\left(\frac{r_{\omega}}{r_{M}}-\left(\frac{r_{\omega}}{r_{M}}\right)^{2}\right) \] 这个是一个凸的二次函数,也就是在中心部位的频率最容易被掩蔽。
目标模式
选定一个目标频率\(r_C\)以及另一个参数\(\sigma_{\Delta}\),定义掩蔽的范围是\(\left[r_{C}-\delta_{I}, r_{C}+\delta_{O}\right]\),\(\delta_{I}\)与\(\delta_{O}\)都是服从一个高斯分布\(f_{\Delta}(\delta)=\sqrt{2} / \sqrt{\pi \sigma_{\Delta}^{2}} e^{-\delta^{2} /\left(2 \sigma_{\Delta}^{2}\right)}, \forall \delta \geq 0\)。在这种模式下,频率\(r_C\)总是被掩蔽,远离\(r_C\)的频率越来越不可能被掩蔽,并具有正态分布的衰减。
中心模式用于SR任务,而目标模式用于denoising。前者有一个缓慢的凹概率衰减,允许覆盖更宽的波段,而后者有一个指数衰减适应于目标非常狭窄的波段。在这两种情况下,最高的频率最有可能被掩盖,较低的频率被衰减概率掩盖。(这句话我没理解,中心模式下,不应该是\(\frac {r_M} 2\)下才是最高概率吗)
实验结果
实际应用中,作者对50%的数据集进行了SFM,得到的效果都比原来好了很多。
这是使用双三次退化、高斯模糊的LR图片测试结果:
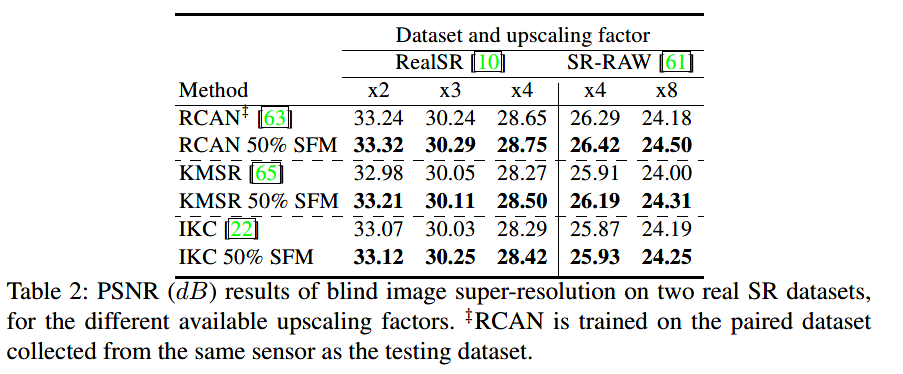
使用真实场景下的退化数据集RealSR和SR-RAW:

加性高斯白噪声的去噪:
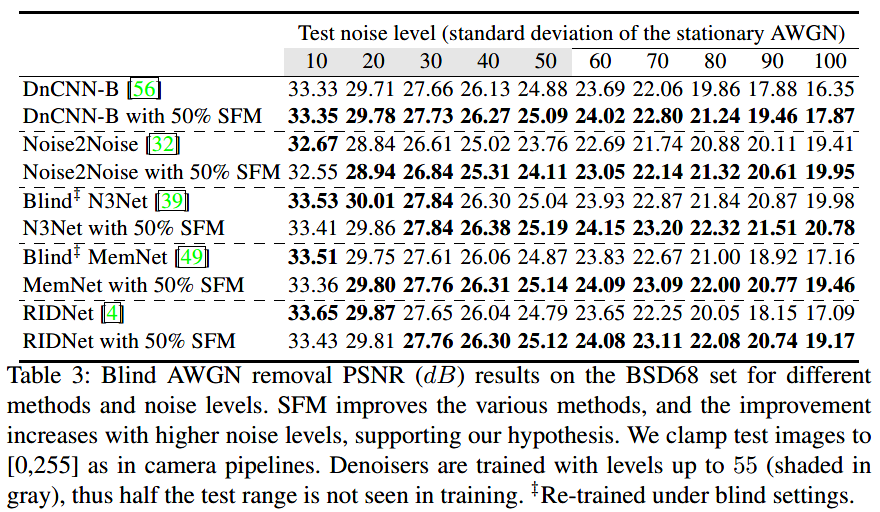
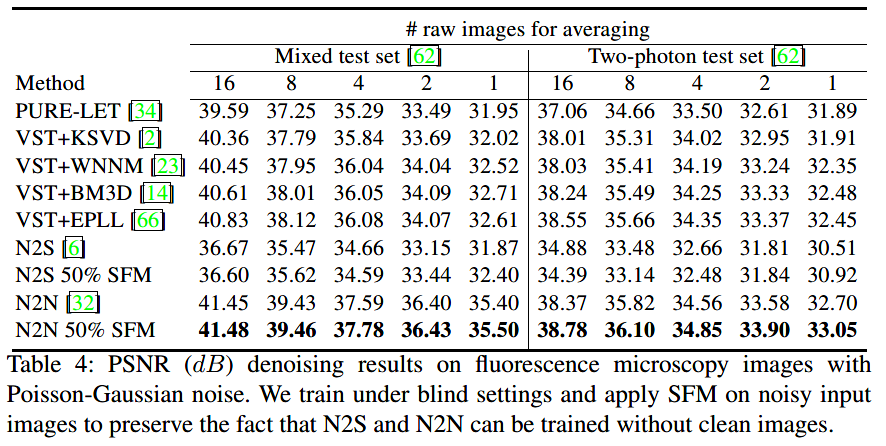
真实的泊松-高斯噪声图片:
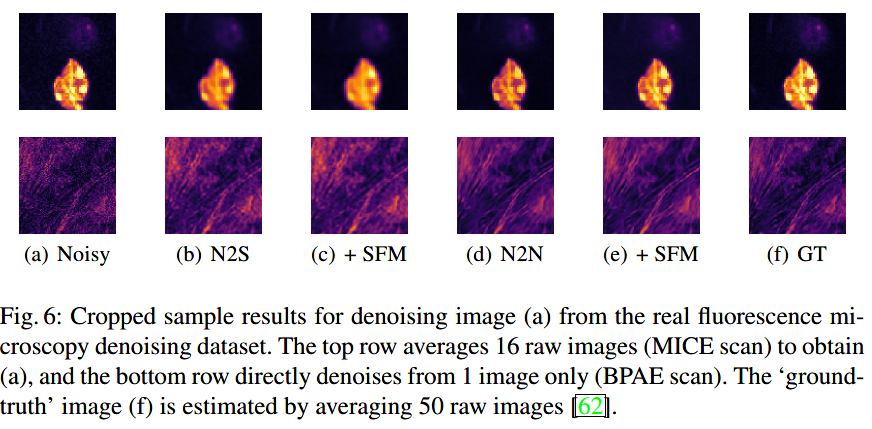
总结与思考
- 这篇工作本身并没有特别复杂,但是从频域角度进行数据增强的思路倒是比较新颖
- 作者设置了巧妙的实验,并通过功率谱密度图,说明了频域下图像复原的条件学习,进而引导出随机频率掩蔽的方法
