论文背景
这篇文章的主要思想是利用对偶学习的思想去训练SR网络，涉及到了很多对偶学习的概念，在这里做一些归纳。
对偶学习(dual learning)
对偶学习最早是在面对机器翻译问题提出来的，发表在Dual Learning for Machine Translation这篇文章里。作者观察到在机器学习的任务中，有许多任务是对偶存在的，比如：英汉互译。现实中我们往往分别考虑两个过程，即对于汉语翻译成英语进行一个模型的训练，对于英语翻译成汉语进行另一个模型的训练。那这两个模型之间是否存在着什么关系呢？是否可以同时训练这两个过程，同时两者之间可以相互的促进？
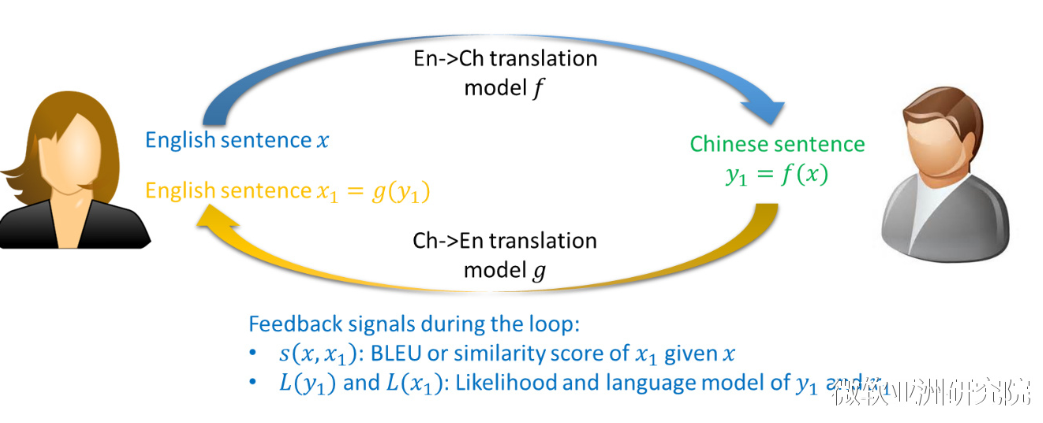
对偶学习的基本思想是两个对偶的任务能形成一个闭环反馈系统，使我们得以从未标注的数据上获得反馈信息，进而利用该反馈信息提高对偶任务中的两个机器学习模型。该思想具有普适性，可以扩展到多个相关任务上面，前提是只要它们能形成一个闭环反馈系统。例如，从中文翻译到英文，然后从英文翻译到日文，再从日文翻译到中文。另外一个例子是从图片转化成文字，然后从文字转成语音，再从语音转化成图片。本文把超分辨问题也看做的一个闭环反馈系统，即LR<—>HR，进而采用了对偶学习的方法。
motivation
- 对于LR->HR这一ill-pose问题，可能的函数空间过大，限制了学习性能。对于这种问题，现有的很多方法的解决方案是提升模型容量，比如EDSR、DBPN、RCAN。但由于函数空间过大，这些方法的性能还是不高，具体体现在难以生成尖锐的纹理(sharp textures) 。因此本文的第一个motivation在于如何减少LR->HR映射空间的大小。
- 对于训练集，当没有paired训练集时，很多SR模型就没用。再者，对于paired训练集，很多真实世界下的LR图片和训练集中使用固定退化形成的LR图片的分布不一样，进而导致模型在自然场景下表现不好。因此，本文的第二个motivation在于如何有效的利用unpaired数据集进而使SR模型更适应实际应用。
主要贡献
- 开发了一个对偶回归方案，使映射可以形成一个闭环，通过对LR图像的重建来提高SR模型的性能。此外，还从理论上分析了该方法的泛化能力，进一步证明了该方法相对于现有方法的优越性。
- 通过提出的双重回归方案，深度模型可以很容易地适应现实世界的数据。
- 通过对训练数据和非配对真实数据的大量实验，证明了对偶回归方法在图像超分辨方面的有效性。
方法详述
对于paired数据的对偶回归
引入两个网络P和D，loss如下：
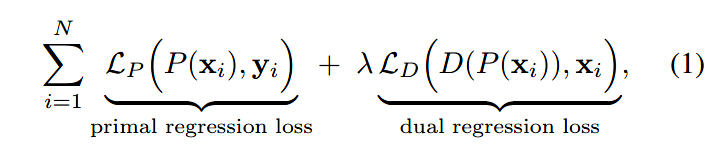
前者是原始回归的损失，用于优化P网络；后者是对偶回归的损失，用于优化D网络。
对于unpaired数据的对偶回归
对于unpaired数据，网络和上述一直，只是loss没有了原始回归的部分。
为了结合paired和unpaired的数据，对于两者混合的数据集，loss如下：
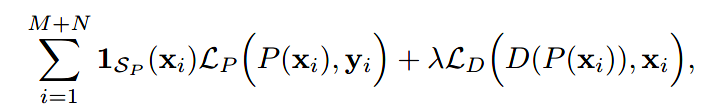
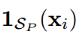当xi属于paired数据时为1，否则为0.
网络结构
整体的网络是带skip connection的U-Net，没有特别的地方：
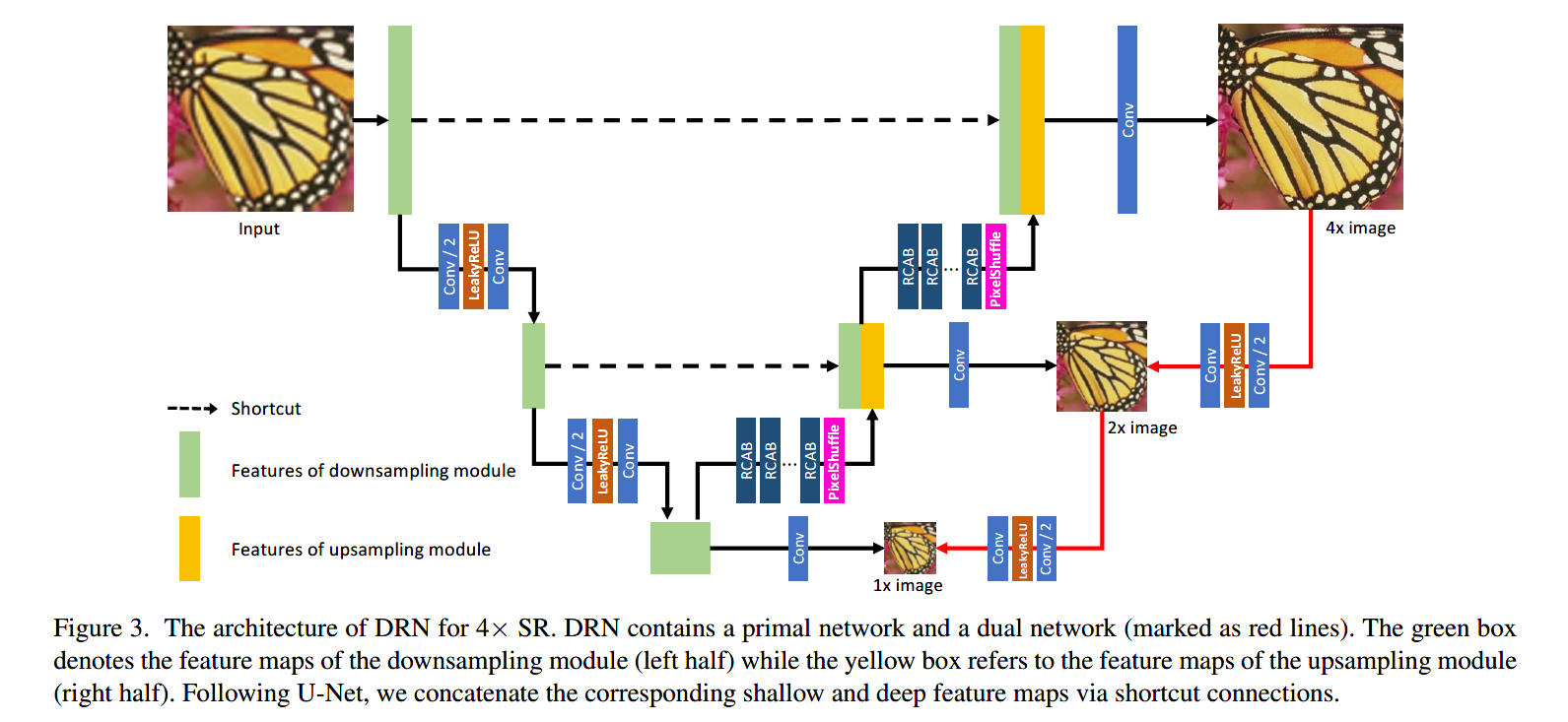
注：U-net左边的input是LR图片通过Bicubic kernel来放大的。
理论分析
本篇论文花了较大篇幅证明这种Dual regression对模型的泛化能力的提升，其中涉及到了Rademacher复杂度等机器学习理论的知识。
推导的结论是：与传统的SR方法相比，对偶回归SR方法具有更小的泛化边界，有助于实现更准确的SR预测。
实验结果
只使用paired数据集
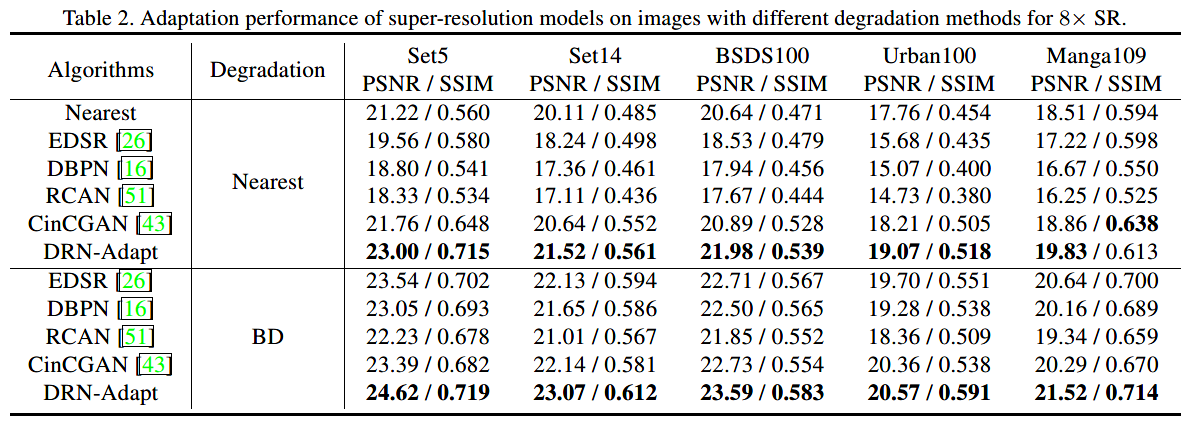
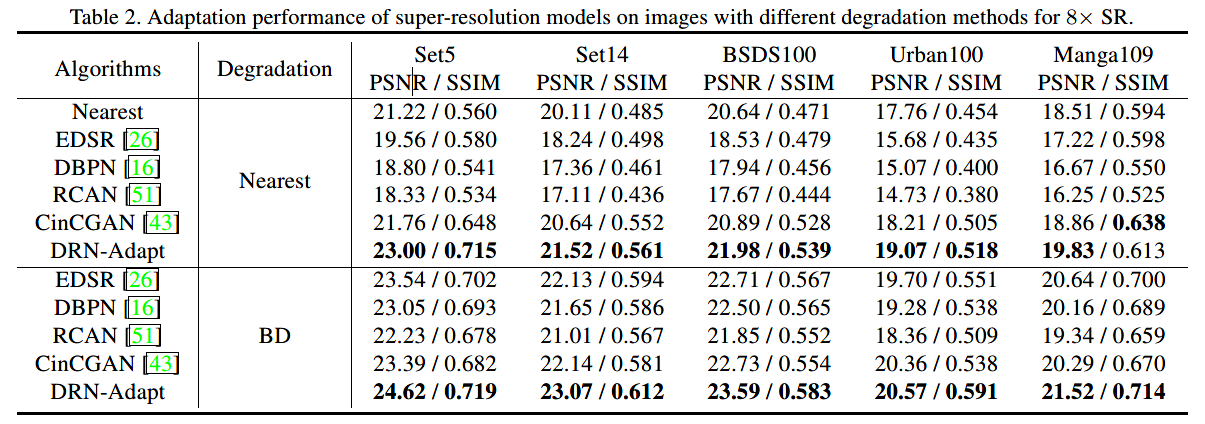
加上unpaired数据
在人工的LR图像的数值表现
在自然图像的视觉表现
消融实验
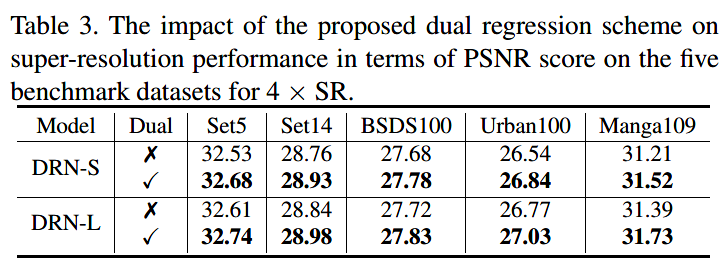
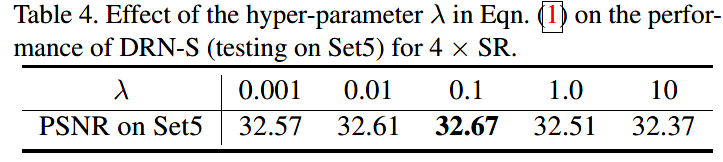
损失函数中的λ取值实验
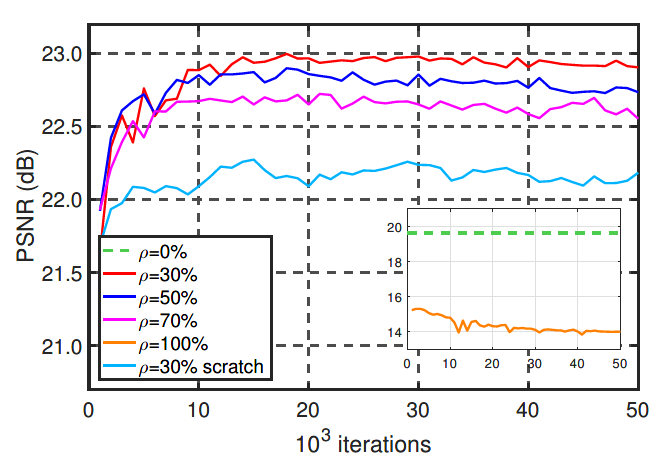
unpaired数据在数据集中的占比ρ
总结与思考
- 乍一看觉得dual regression的思路跟上周看的基于Cycle-GAN的方法的机制很像，但是本文中作者也特地强调了区别：
- 基于Cycle-GAN的方法，使用循环一致损失是为了防止在domain transfer的时候模型倒塌(mode collapse)（即把所有的图片都映射为同一张图来骗过discriminator）；而本文中的目的是把“闭环”作为一个额外的约束来减小可能的函数空间。
- 基于Cycle-GAN的方法完全抛弃了成对的合成数据(paired synthetic data)；但是本文可以同时利用成对的合成数据和真实世界的非成对数据来增强训练。
- 本文出现了很多数学推导，特别是函数空间、Rademacher复杂度等概念我之前没有接触过，读起来比较吃力，而且理解得不是很深刻。让我体会到了自己的机器学习基础数学理论还需要加强。