指的是列向量
矩阵求导
矩阵求导在最大似然问题中经常出现。总的来说,矩阵求导有四种类型,可以用下列表格表示:
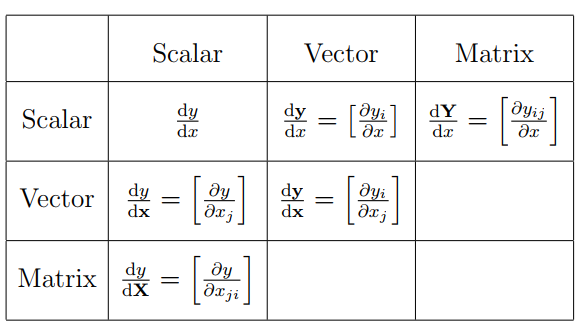
一句话概括:分子的偏导符号根据\(\mathbf{Y}\)的形状展开,而分母的偏导符号根据\(\mathbf{X}\)的形状的转置展开。举例来说,\(\mathrm d \mathbf y / \mathrm{d} x\)是一个列向量,\(\mathrm{d} y / \mathrm{d} \mathbf{x}\)是一个行向量(假设\(\mathbf y\)和\(\mathbf x\)都指的是列向量)。每个积分都可以这样“冗长地”通过标量的偏导来计算,但是本节展示如何来通过矩阵操作来计算矩阵求导。
就像工数中学习的那样,定义微分\(dy(x)\)为增量\(y(x+\mathrm{d} x)-y(x)\)对\(dx\)的线性主部。不像是经典的极限定义,这里的定义即使在\(x\)或\(y\)不是标量的情况下也成立。
举例来说,下面的等式: \[ \mathbf{y}(\mathbf{x}+\mathrm{d} \mathbf{x})=\mathbf{y}(\mathbf{x})+\mathbf{A} \mathrm{d} \mathbf{x}+(\text {更高阶的无穷小项} ) \] 对于任意满足一定连续性的\(\mathbf y\)都有定义。式中的矩阵\(\mathbf A\)就是导数,又叫做雅可比矩阵\(\mathbf{J}_{x \rightarrow y}\)。它的转置即为\(y\)的梯度\(\nabla \mathbf{y}\)。雅可比矩阵在微积分中很有用,而梯度在优化问题中很有用。
因此,对于任意表达式的导数都可以用两个步骤来计算:
- 计算其微分
- 把结果写成规范的形式
然后矩阵导数就能够从\(\mathrm{d} x, \mathrm{~d} \mathbf{x},\) 或者\(\mathrm{d} \mathbf{X}\)的系数中直接读出。
第二步规范化的过程可以通过以下定理来完成: \[ \mathrm{dA}=0 \text { (for constant } \mathbf{A}) \]
\[ \mathrm{d}(\alpha \mathbf{X})=\alpha \mathrm{d} \mathbf{X} \]
\[ \mathrm{d}(\mathbf{X}+\mathbf{Y})=\mathrm{d} \mathbf{X}+\mathrm{d} \mathbf{Y} \]
\[ \mathrm{d}(\operatorname{tr}(\mathbf{X}))=\operatorname{tr}(\mathrm{d} \mathbf{X}) \]
\[ \mathrm{d}(\mathrm{XY})=(\mathrm{d} \mathrm{X}) \mathrm{Y}+\mathrm{XdY} \]
\[ \mathrm{d}(\mathrm{X} \otimes \mathrm{Y})=(\mathrm{d} \mathrm{X}) \otimes \mathrm{Y}+\mathrm{X} \otimes \mathrm{d} \mathrm{Y} \quad \text { (see section 2) } \]
\[ \mathrm{d}(\mathrm{X} \circ \mathrm{Y})=(\mathrm{d} \mathrm{X}) \circ \mathrm{Y}+\mathrm{X} \circ \mathrm{d} \mathrm{Y} \quad(\text {see section } 5) \]
\[ \mathrm{d} \mathbf{X}^{-1}=-\mathbf{X}^{-1}(\mathrm{~d} \mathbf{X}) \mathbf{X}^{-1} \]
\[ \mathrm{d}|\mathbf{X}|=|\mathbf{X}| \operatorname{tr}\left(\mathbf{X}^{-1} \mathrm{~d} \mathbf{X}\right) \]
\[ \mathrm{d} \log |\mathbf{X}|=\operatorname{tr}\left(\mathbf{X}^{-1} \mathrm{~d} \mathbf{X}\right) \]
\[ \mathrm{d} \mathbf{X}^{\star}=(\mathrm{d} \mathbf{X})^{\star} \]
(12)式中的*指的是任意对元素的重排操作,比如转置、向量化、向量化-转置等。
以上大多数规则可以通过计算\(\mathbf{F}(\mathbf{X}+\mathrm{d} \mathbf{X})-\mathbf{F}(\mathbf{X})\),然后取线性主部来导出,比如(6)式: \[ \because (\mathbf{X}+\mathrm{d} \mathbf{X})(\mathbf{Y}+\mathrm{d} \mathbf{Y})=\mathbf{X} \mathbf{Y}+(\mathrm{d} \mathbf{X}) \mathbf{Y}+\mathbf{X} \mathrm{d} \mathbf{Y}+(\mathrm{d} \mathbf{X})(\mathrm{d} \mathbf{Y}) \nonumber \\ \therefore (\mathbf{X}+\mathrm{d} \mathbf{X})(\mathbf{Y}+\mathrm{d} \mathbf{Y})-\mathbf{X} \mathbf{Y}=(\mathrm{d} \mathbf{X}) \mathbf{Y}+\mathbf{X} \mathrm{d} \mathbf{Y}+(\mathrm{d} \mathbf{X})(\mathrm{d} \mathbf{Y}) \\ \therefore \mathrm{d}(\mathbf{XY})=(\mathrm{d} \mathbf{X}) \mathbf{Y}+\mathbf X \mathrm d\mathbf Y \] 而要导出\(\mathrm d\mathbf{X}^{-1}\),可以通过下式导出: \[ 0=\mathrm{d} \mathbf{I}=\mathrm{d} \mathbf{X}^{-1} \mathbf{X}=\left(\mathrm{d} \mathbf{X}^{-1}\right) \mathbf{X}+\mathbf{X}^{-1} \mathrm{~d} \mathbf{X} \]
下一步,把微分推导为以下六种规范形式(假设\(\mathbf x\)和\(\mathbf y\)都是列向量):
