经过上次旁听小组会,大致对神经表示的方法有所了解,这是那次组会上张江辉分享的神经表示+超分辨的论文,当时没有太听明白,这回拿出来仔细研读一下。
这篇论文主要利用了神经表示在3D重构中的作用,提出了一个局部隐式图像函数(Local Implicit Image function, LIIF),利用表示的连续性完成任意尺度的超分辨。
论文背景
真实的视觉世界应该是连续的,但是机器在捕获一个场景的图片时,会将其离散化采样为2D得像素数组,也就是基于像素表示的数字图像。而这种表示方法也带来了“分辨率”这一衡量图像采样质量的描述。而本文的工作是想以一种连续性的表示方法去表示图像,这样,我们可以以任意的分辨率来储存、生成图像。
对于连续地表示图像,经典的编码器-解码器就是一个例子——把图像编码到一个隐空间,这个隐空间就是连续的,再通过一个独立的解码器解码出图像。但作者表示,这种encoder是在实例(instance)之间分享知识(knowledge)的,这里我的理解是encoder是学习了不同的图像(实例)的编码过程,得到了最终的encoder参数(知识),也就是多个实例共享一个decoder模型的。而decoder也是一样的道理。但是这种表示方法,只能成功地表示简单的图像,无法表示信息丰富的自然图像。据作者推断,这是因为,将自然图像的所有细节编码在一个简单的隐编码中是很困难的。
然后作者基于神经表示的思想,在本文提出一个局部隐式图像函数(Local Implicit Image function, LIIF),用一组分布在空间维度上的隐码来表示图像,每个隐码存储关于其局部区域的信息。
对于这样一种表示方法,其输入也是一张基于像素表示的离散图像吗,但是LIIF却要生成准确度更高的信息,于是
方法详述
局部隐式图像函数(Local Implicit Image function, LIIF)
在LIIF的表示中,\(I^{(i)}\)表示连续图像,而这个\(I^{(i)}\)是由一个二维的特征图\(M^{(i)} \in \mathbb{R}^{H \times W \times D}\)变换而来的,而一个建模成MLP的神经隐式函数定义为如下: \[ s=f(z, x) \] 其中\(z\)是一个特征向量,\(x \in \mathcal{X}\) 是一个二维连续坐标,\(s \in \mathcal{S}\) 是预测的RGB值。这样,每个\(z\)都可以被看做一个二维坐标到像素值的一个映射:\(f(z, \cdot): \mathcal{X} \mapsto \mathcal{S}\),而这个映射本身\(f(z, \cdot)\)正是一种图像的连续的表示。假设\(H\times W\)个\(D\)维特征向量(后文中称为latent code隐码)均匀地分布在连续图像\(I^{(i)}\)所在的二维空间中,组成了特征图\(M^{(i)}\)。
更具体地,对于连续图像\(I^{(i)}\),在坐标\(x_q\)处的RGB值可表示为: \[ I^{(i)}\left(x_{q}\right)=f\left(z^{*}, x_{q}-v^{*}\right) \] 其中,\(z^*\)是离坐标\(x_q\)处欧氏距离最近的latent code,\(v^*\)是\(z^*\)的坐标,那么\(x_q-v^*\)也就是一个坐标偏移(欧式空间中的向量)。
另外,作者为LIIF设置了如下几个trick:
特征折叠(Feature unfolding)
为了使得隐码包含更多的空间局部信息,其实就是把原始的\(M^{(i)}\)的每个3x3相邻的隐码concatenate到一起。
Feature unfolding
式(2)存在一个问题,当目标点的位置从一个\(z\)的附近渐变到另一个\(z\)的附近时,\(z^*\)的选取会发生改变,从而造成像素值的突变,这会大大影响到图像的局部像素值连续性。
对此,作者提出了Feature unfolding的方法,其实就是通过多个\(f(\cdot)\)的加权和,扩大\(z\)的选取范围为离离坐标\(x_q\)处欧氏距离最近的4个latent code。而根据到坐标\(x_q\)处的相对距离不同,有不同的权值。 \[ I^{(i)}\left(x_{q}\right)=\sum_{t \in\{00,01,10,11\}} \frac{S_{t}}{S} \cdot f\left(z_{t}^{*}, x_{q}-v_{t}^{*}\right) \]
Cell decoding
设想使用LIIF的表示方法解码出任意分辨率的离散图像的场景,直接的做法是根据所需分辨率,均匀离散地取各个坐标,代入LIIF中查询得到各点的像素值。但是这种做法有一个问题,某个点的查询所得像素值是独立于目标图像分辨率的,换句话说,无论是什么分辨率,该点的像素值都是一成不变的,也就是说,其他更精细尺度下的信息在某个粗糙尺度下被完全丢弃了,这其实是不符合常规的图像退化假设的。比如高分辨到低分辨的退化中,并不是单纯的下采样,而是首先伴随一个模糊的过程(双三次、任意模糊核等待),也就是一个整合周围像素信息的过程,而已定义的LIIF把这个过程忽略掉了。
于是作者把图像分辨率信息也加入到LIIF中,具体做法是,把图像长宽的倒数与坐标\(x_q\)连接在一起: \[ s=f_{\text {cell }}(z,[x, c]) \]
学习过程
学习过程可以用下图概括:
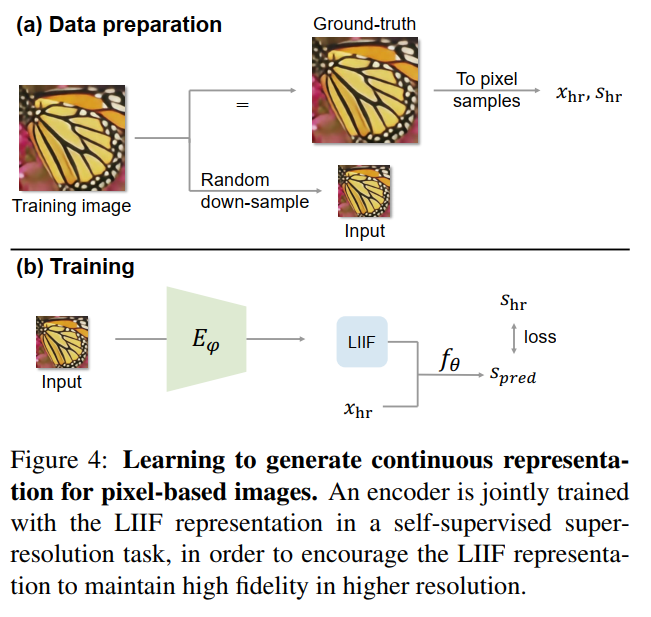
由原始的图像作为GT,采样点坐标为\(x_{hr}\),对应的像素值为\(s_{hr}\),然后进行监督训练。此处loss为L1 loss。
实验设计与结果
训练数据集为DIV2K,把EDSR、RDN去除最后的Upsample模块,作为\(E_{\varphi}\)的结构。
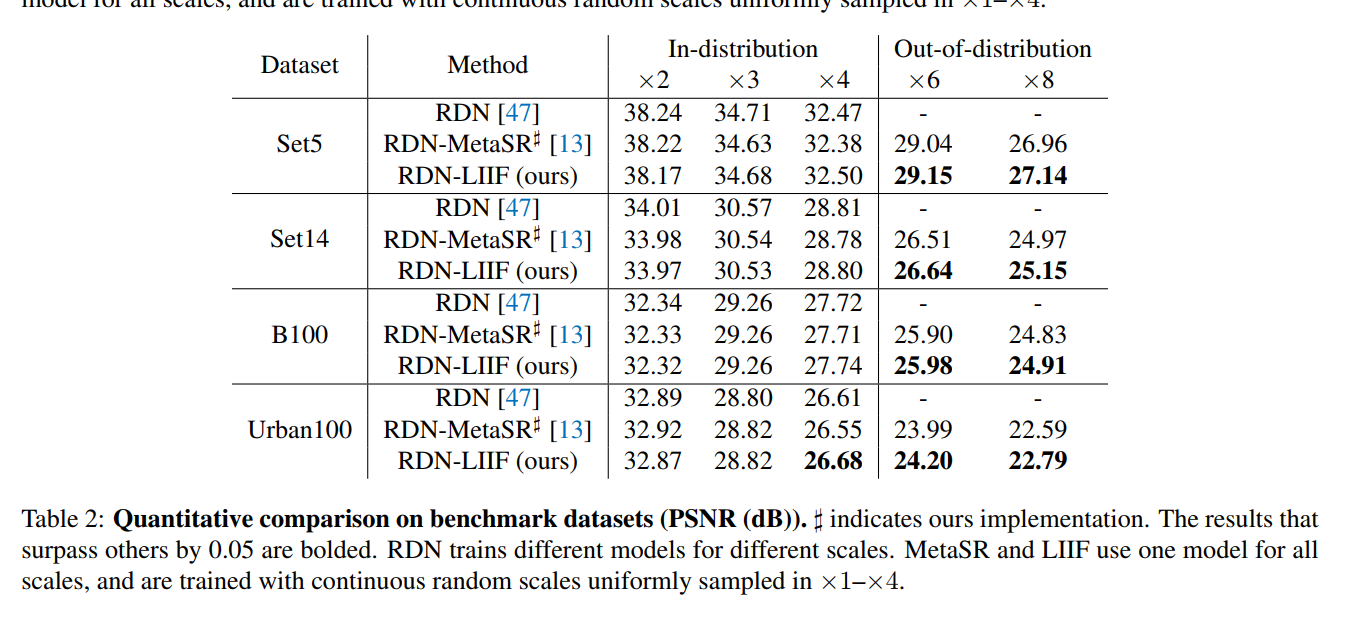
总结与思考
- 这是一篇把神经表示应用到超分辨领域的工作,应用的角度也很直接,就是把3D的神经表示应用到2D图像中
- 不过其没有直接使用一个MLP去强行表示一幅LR图像,而是充分利用了SOTA的SR网络起到的特征提取能力,将提取的特征图作为LIIF的输入,利用超分辨退化的局部性,设置了LIIF的变换过程。
- 换个角度说,其实LIIF就是一个可变的上采样模块,用于替换EDSR等SOTA SR网络的上采样层。只不过在推理过程中,后续的LIIF网络参数是“LR输入相关的”,对于每个LR输入,都需要把上采样层的参数进行重新训练。
- 我觉得这种模型最大的优点是,对于同一张测试图像下,变换尺度的效率很高,因为只需要更改连续坐标的采样间隔即可。但是对于不同的测试图像,需要额外的时间训练其神经表示,时间效率不高,不过这也是神经表示本身的缺点之一
- 其余的特征折叠(Feature unfolding)、Feature unfolding、Cell decoding基本算是根据SR任务的特征加入的小trick
$$
$$