这是一篇超分领域的知识蒸馏工作,发表于ECCV 2020
论文背景
传统的CNN-based超分方法,一般需要大量的存储资源和计算资源,难以在移动设备以及一些没有神经处理单元和芯片外存储器的设备上运行。
也有很多工作是致力于减少神经网络的消耗的:
- 比如在SISR中,使用递归层或者一些专门为SISR设计的网络结构。但是这些递归层或者专门设计的结构难以在硬件上实现。
- 网络剪枝、参数量化也被用于网络压缩。其中网络剪枝去除了一些节点冗余连接,而参数量化则降低权重或激活函数的位精度。然而,网络剪枝使得存储访问不连续,而且数据的局部性也较弱,这大大降低了性能。而网络量化的性能本质上取决于全精度模型的性能。
- 模型压缩的另一种方式是知识蒸馏(Knowledge distillation),即一个大型的模型(teacher网络)软化版本输出分布(即logit)或中间特征表示,由一个小网络(student网络),这在图像分类任务中已经表现出有效性。而广义蒸馏(teacher)更进一步允许teacher网络)在训练时利用额外的信息(优势特征),并用补充的知识辅助学生网络的训练过程
本论文的主要idea就是,ground-truth HR图像,可以看作为一个优势信息(privileged information)。的确,HR图像包含了LR图像中缺乏的成分(如高频特征),但是,现有的SISR方法,仅仅把它用作用于惩罚重构错误程度。与之相对比,作者提出的方法,使用HR图像作为优势信息,允许提取互补特征,并明确地将它们用于SISR任务。为了实现这个idea,作者设计了一个知识蒸馏的框架,框架中,teacher网络和student网络都致力于重构HR图像,却使用了不同的输入:teacher网络的输入是GT HR图像,而student网络的输入时对应的LR图像——这与传统的知识蒸馏框架是不同的。
具体框架如下图:
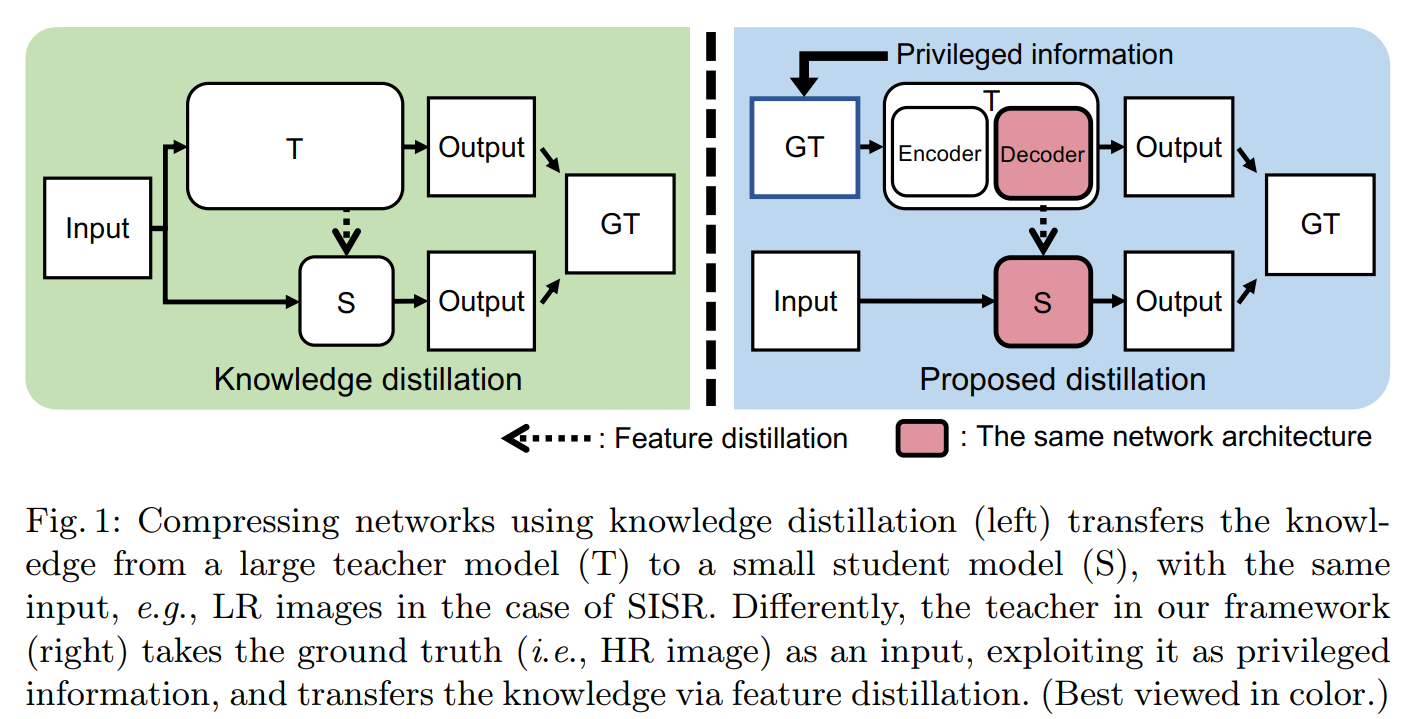
传统的知识蒸馏方式如左图,其T网络和S网络的输入是一样的。而本文采用的广义蒸馏方式,对于T网络,其输入是一个优势特征——HR图像,而Encoder-Decoder的沙漏结构,其中的Decoder即为S网络的学习对象,Decoder中的中间特征通过特征蒸馏传递给S网络,这样S网络就可以学习通过优势特征培训的T网络的知识(例如,高频或HR输入的细节)。S网络可以用解码器的网络参数初始化,这允许将教师的重构能力转移给S网络。(?)
方法详述
Teather网络
由于教师网络输入的是真实的HR图像,可能无法提取出有用的特征,不管其容量如何,只是学会复制其输入——HR图像。此外,网络参数数量的巨大差异或教师和学生之间的表现差距阻碍了蒸馏过程。
为了在促进Teather网络获取有用特征的同时减少差距,作者为Teather网络开发了一个沙漏结构。将HR图像投影到一个低维的特征空间中,生成紧凑的特征,然后从这些特征中重构出原始HR图像,这样Teather网络就可以学习提取更好的特征表示来完成图像重构任务。具体来说,教师网络由一个编码器\(G^{\mathcal{T}}\)和一个解码器\(F^{\mathcal{T}}\)组成。给定一对LR和HR图像,编码器\(G^{\mathcal{T}}\)将输入HR图像\(\mathbf Y\)转换为特征表示\(\hat{\mathbf{X}}^{\mathcal{T}}\)。 \[ \hat{\mathbf{X}}^{\mathcal{T}}=G^{\mathcal{T}}(\mathbf{Y}) \] 而\(\hat{\mathbf{X}}^{\mathcal{T}}\)的size和LR图像是一致的,decoder把\(\hat{\mathbf{X}}^{\mathcal{T}}\)重新重构为HR图像\(\hat{\mathbf{Y}}^{\mathcal{T}}\)。 \[ \hat{\mathbf{Y}}^{\mathcal{T}}=F^{\mathcal{T}}\left(\hat{\mathbf{X}}^{\mathcal{T}}\right) \] 对于decoder,使用与Student网络相同的架构。它允许教师拥有与学生相似的表现能力,这在《Improved knowledge distillation via teacher assistant: Bridging the gap between student and teacher》(AAAI 2020)中被证明是有用的。
而损失函数即为重构损失+模仿损失(imitation loss): \[ L_{\mathrm{recon}}^{\mathcal{T}}=\frac{1}{H W} \sum_{i=1}^{H} \sum_{j=1}^{W}\left|Y_{i j}-\hat{Y}_{i j}^{\mathcal{T}}\right| \]
\[ L_{\mathrm{im}}^{\mathcal{T}}=\frac{1}{H^{\prime} W^{\prime}} \sum_{i=1}^{H^{\prime}} \sum_{j=1}^{W^{\prime}}\left|X_{i j}-\hat{X}_{i j}^{\mathcal{T}}\right| \]
Student网络
student网络完成以下映射: \[ \hat{\mathbf{Y}}^{\mathcal{S}}=F^{\mathcal{S}}(\mathbf{X}) \] 损失函数使用的是重构损失+蒸馏损失。重构损失如下: \[ L_{\text {recon }}^{\mathcal{S}}=\frac{1}{H W} \sum_{i=1}^{H} \sum_{j=1}^{W}\left|Y_{i j}-\hat{Y}_{i j}^{S}\right| \]
蒸馏损失
用\(\mathbf{f}^{\mathcal{T}}\)和\(\mathbf{f}^{\mathcal{S}}\)分别表示教师网络和学生网络的中间特征,它们的大小相同,分别为\(C×H'×W'\),定义互信息(mutual information)如下: \[ I\left(\mathbf{f}^{\mathcal{T}} ; \mathbf{f}^{\mathcal{S}}\right)=H\left(\mathbf{f}^{\mathcal{T}}\right)-H\left(\mathbf{f}^{\mathcal{T}} \mid \mathbf{f}^{\mathcal{S}}\right) \] \(H\left(\mathbf{f}^{\mathcal{T}}\right)\)和\(H\left(\mathbf{f}^{\mathcal{T}} \mid \mathbf{f}^{\mathcal{S}}\right)\)分别是边际熵和条件熵(marginal and conditional entropies)。为了使互信息最大化,应该使条件熵\(H\left(\mathbf{f}^{\mathcal{T}} \mid \mathbf{f}^{\mathcal{S}}\right)\)最小。然而,对学生的权重进行精确的优化是很难的,因为它涉及到对条件概率\(p\left(\mathbf{f}^{\mathcal{T}} \mid \mathbf{f}^{\mathcal{S}}\right)\)的积分。变分信息最大化(The variational information maximization)技术使用参数模型\(q\left(\mathbf{f}^{\mathcal{T}} \mid \mathbf{f}^{\mathcal{S}}\right)\)来近似条件分布\(p\left(\mathbf{f}^{\mathcal{T}} \mid \mathbf{f}^{\mathcal{S}}\right)\),例如高斯分布或拉普拉斯分布,使得找到互信息\(I\left(\mathbf{f}^{\mathcal{T}} ; \mathbf{f}^{\mathcal{S}}\right)\)的下界。对于参数模型\(q\left(\mathbf{f}^{\mathcal{T}} \mid \mathbf{f}^{\mathcal{S}}\right)\),我们使用一个多元拉普拉斯分布,这个分布包含两个参数,其中\(\boldsymbol{\mu}\)为位置参数,而\(\boldsymbol b\)为尺度参数(控制蒸馏的程度),\(\boldsymbol{\mu},\boldsymbol{b} \in \mathbb{R}^{C \times H^{\prime} \times W^{\prime}}\)。于是定义蒸馏损失\(L_{\text {distill }}^{S}\)为: \[ L_{\mathrm{distill}}^{\mathcal{S}}=\frac{1}{C H^{\prime} W^{\prime}} \sum_{i=1}^{C} \sum_{j=1}^{H^{\prime}} \sum_{k=1}^{W^{\prime}} \log b_{i j k}+\frac{\left|f_{i j k}^{\mathcal{T}}-\mu_{i j k}\right|}{b_{i j k}} \] 当S网络不能从蒸馏中获益时,尺度参数\(b_{ijk}\)增大以减小蒸馏程度。因为教师和学生网络采取不同的输入,这样就能自适应地决定,学生从教师那里学到学生“可以接受的”特征。\(\log b_{i j k}\)相当于一个正则项,防止\(b_{i j k}\)造成loss的一个平凡解。
而\(\boldsymbol{\mu}\)和\(\boldsymbol{b}\)是从student网络的特征\(\mathbf f^{\mathcal S}\)中估计的。估计方法是使用一个小网络,这个小网络有两个分支,分别用于估计\(\boldsymbol{\mu}\)和\(\boldsymbol{b}\)。两个分支使用相同的网络架构,两个1×1卷积层,之间有一个PReLU。对于估计\(\boldsymbol{b}\)的尺度分支,我们在最后一层添加softplus函数(ζ(x) = log(1 + e^x)),使尺度参数为正。注意,估算模块是为蒸馏过程服务的,因此仅在训练时使用。
实验设计与结果
与大多数SR工作一样,使用DIV2K来训练,并在Set5、Set14、B100、Urban100上做测试。
消融实验
如下表所示。
- baseline使用的是FSRCNN(第一行)。
- 从第二行开始,就能看出distillation对SR结果的促进效果了。第二行是把FSRCNN的结构去掉最后的deconvolution,作为teacher的结构,但没有沙漏结构。
- 而第三行的沙漏结构限制了教师的性能并降低了性能(例如:第二排的老师比第二排的老师下降了19.9dB),但是缩小了老师和学生之间的成绩差距。这使得特征提取更加有效,因此第三行student的性能(37.22dB)优于第二行student的性能(37.19dB)。
- 从第四行可以看出,学生网络从教师中解码器的网络权值初始化中获益,这为学习提供了一个良好的起点,并转移了教师的重构能力。
- 第五行,模仿损失进一步提高了PSNR的性能,使得学生更容易从老师那里学习特征。
- 最后两行表明,在拉普拉斯分布的情况下,VID loss的处理效果比MAE的要好(基于MAE的蒸馏损失,会使得学生网络和教师网络的特征图相同。然而,这种对特征映射的强烈约束在本文的例子中是有问题的,因为本文的框架中对学生和教师网络使用了不同的输入。)
LR
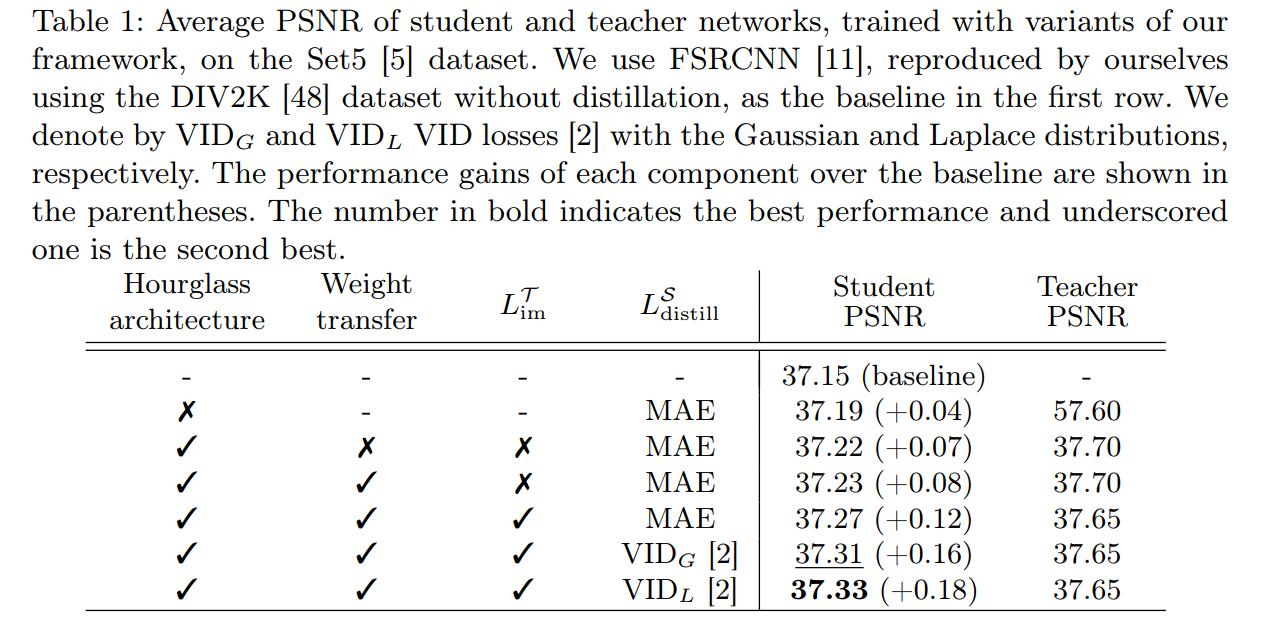
对于encoder编码得到的compact features ,作者也在w和w/o imitation loss的条件下做了分析,这个结果也是可预见的。
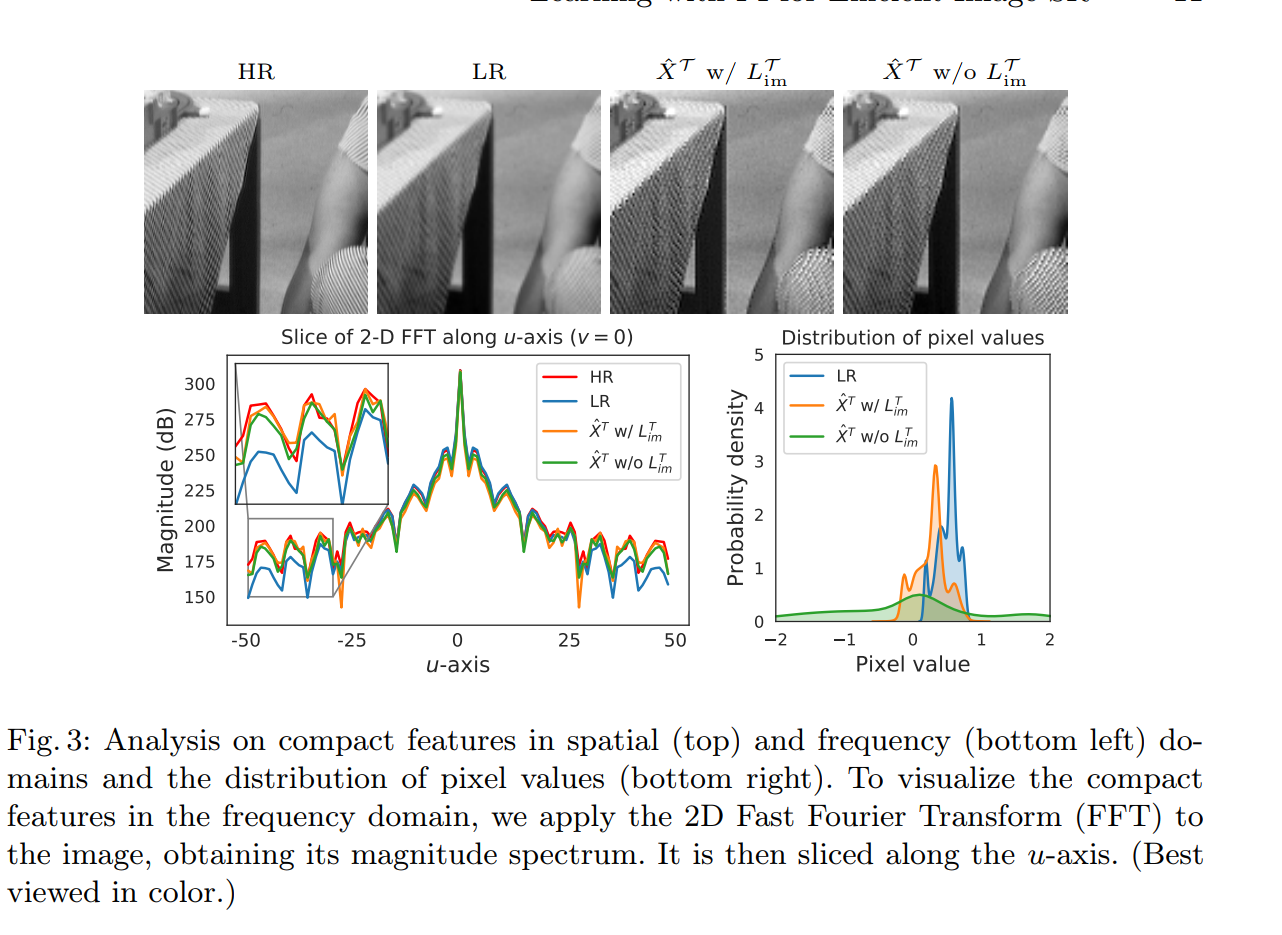
最终结果
最终也是取得了不错的结果。相对于baselineFSRCNN,没有任何参数或是计算量的增加,但提上来了指标。相对于其他的大模型,本框架在时空效率上也更优。
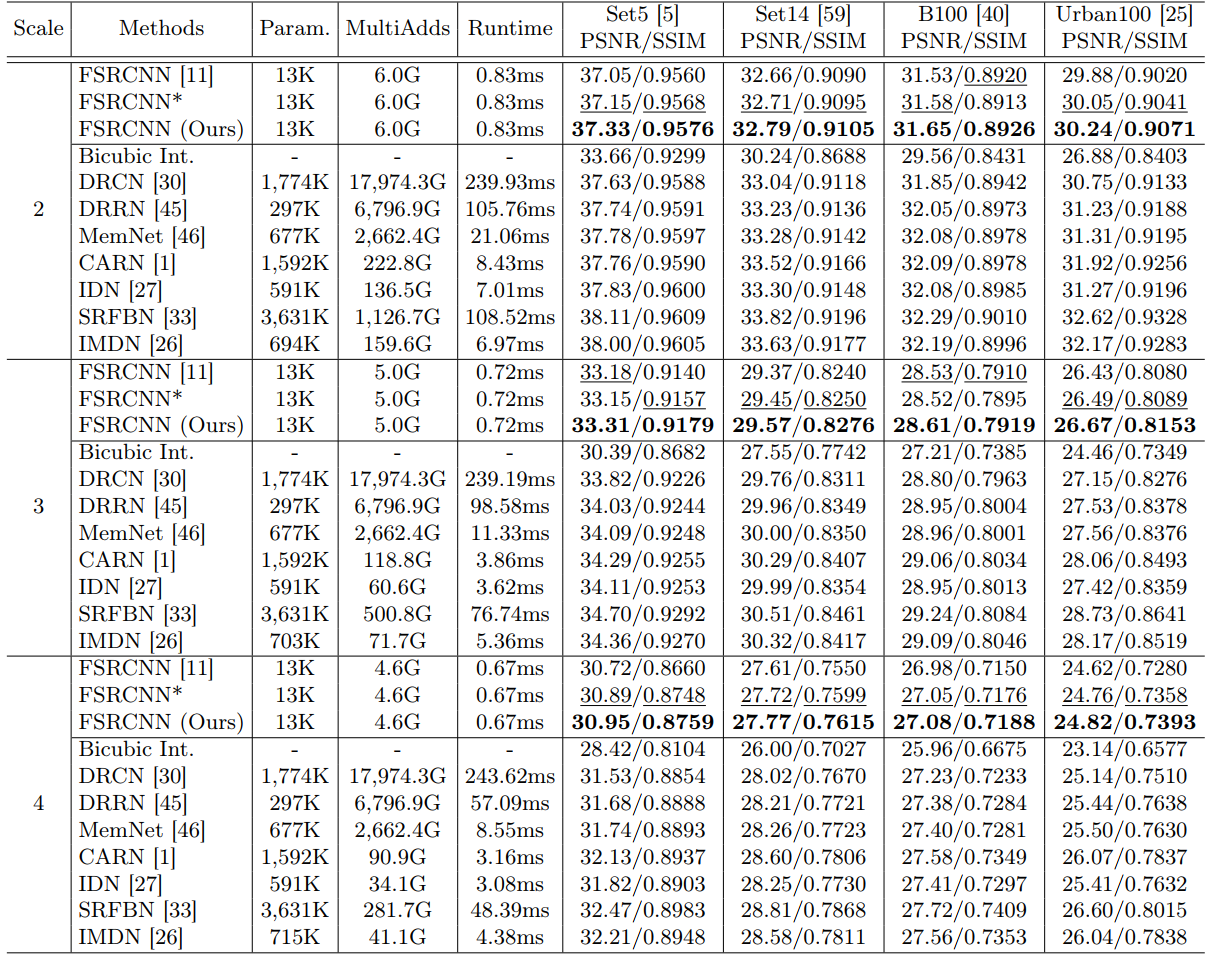
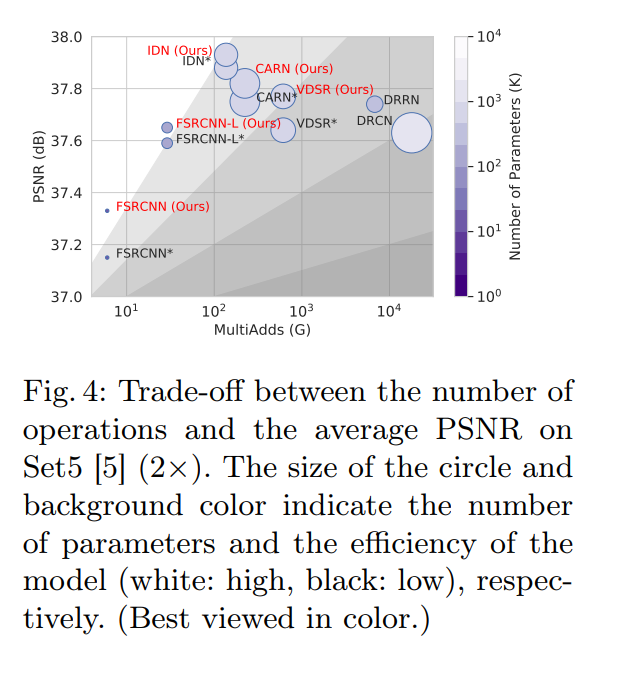
不仅在FSRCNN上,把本方法应用到其他SR模型中,也能提升性能: