论文背景
对于图像超分辨问题,最简单的方法是基于邻像素的空间不变性的双线性插值、双三次插值等方法,但是这些方法忽视了图像内容的多样性,会造成过于模糊的纹理结构与细节。
为了处理图像中的不同的内容,稀疏字典学习(sparse dictionary learning)独立地处理每个像素(或者patch)。比如经典的这篇《Image super-resolution via sparse representation》,给LR和HR中的patch学习一对字典,而假设LR和HR图像共享同一个稀疏编码。在推理过程中,给定训练字典,在一个优化过程中求出稀疏编码,从而完成对HR的估计。然而,在训练过程中,(字典与编码的)联合优化的难度还是会影响恢复效果。比如《Raisr: Rapid and accurate image super resolution》这篇中,基于图像的局部梯度统计特征,对图像的patch进行聚类处理,对每一类使用一个滤波器。虽然简单,但这种硬选择(hard-selection)操作是不连续的且不可微的。它们只为变化的输入模式提供折衷的解决方案,而不是最优的解决方案。
而之后,各类深度学习的方法被提出来,但是挑战在于图像内容的无约束性质,当随机梯度存在很大变化时,训练可能是不稳定的。它会导致artifact。残差学习、注意力机制等策略可以缓解这些问题,但这些方法对计算资源要求很高。
与对原图像的直接估计不同,自适应滤波器(核)方法按照空间变化,对相邻像素进行分组。由此带来的好处有两点:
- 估计的像素始终处于环境的凸包内,为了避免视觉伪影的产生(?)
- 网络只需要评估相邻像素的相对重要性,而不需要预测绝对值,这加快了学习过程
本文作者提出了一种,对SISR问题进行线性约束的方法——LAPAR(linearly-assembled pixel-adaptive regression network,线性组合像素自适应回归网络)。核心思想是,对一个进行把LR进行Bicubic插值后的模糊图像,应用一个“像素自适应”的滤波器进行滤波。而滤波器来自于,轻量级的卷积神经网络,这个网络根据每个输入像素,确定预定义的滤波器基的线性组合系数。
方法详述
方法没有很复杂,用以下图片就可以看出来
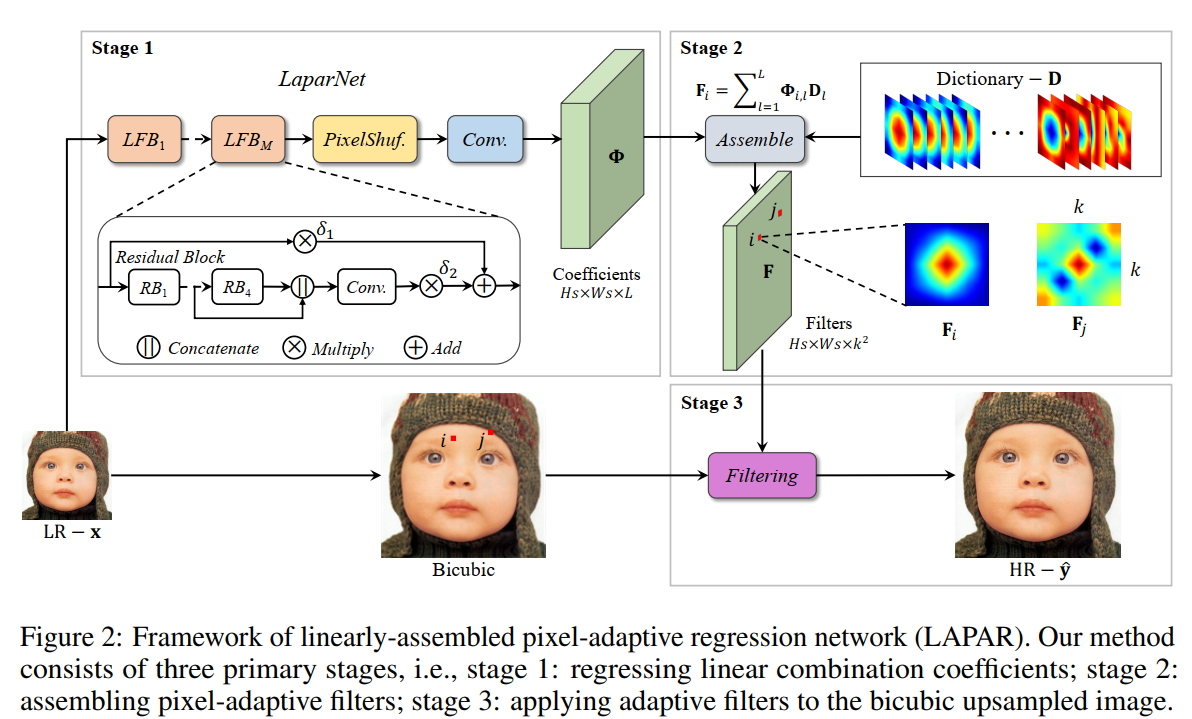
预定义了一堆滤波器字典(也就是线性组合的基)\(\mathbf{D} \in \mathbb{R}^{L \times k^{2}}\),然后设计一个网络LaparNet,输入LR图像,学习每个像素对应的滤波器的系数Coefficients,每个像素所在的Bicubic patch都对应了一个由线性基合成的滤波器(卷积核)。而在实际SR过程中,把Bicubic 插值后的图像,应用每个patch所对应的卷积核,即可恢复出SR图像。
而滤波器字典的采用的都是高斯滤波器(G)和差分高斯滤波器(DoG): \[ \begin{aligned} G\left(\mathbf{x}-\mathbf{x}^{\prime} ; \mathbf{\Sigma}\right)&=\frac{1}{2 \pi|\mathbf{\Sigma}|^{\frac{1}{2}}} \exp \left\{-\frac{1}{2}\left(\mathbf{x}-\mathbf{x}^{\prime}\right)^{T} \mathbf{\Sigma}^{-1}\left(\mathbf{x}-\mathbf{x}^{\prime}\right)\right\} \\ \boldsymbol{\Sigma} &=\gamma^{2} \mathbf{U}_{\theta} \boldsymbol{\Lambda} \mathbf{U}_{\theta}^{T} \\ \mathbf{U}_{\theta} &=\left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right] \\ \boldsymbol{\Lambda} &=\left[\begin{array}{cc} \sigma_{1}^{2} & 0 \\ 0 & \sigma_{2}^{2} \end{array}\right] \\ D o G\left(\mathbf{x}-\mathbf{x}^{\prime} ; \mathbf{\Sigma}_{1}, \mathbf{\Sigma}_{2}\right)&=G\left(\mathbf{x}-\mathbf{x}^{\prime} ; \mathbf{\Sigma}_{1}\right)-G\left(\mathbf{x}-\mathbf{x}^{\prime} ; \mathbf{\Sigma}_{2}\right) \end{aligned} \]
实验结果
首先对于滤波器字典,作者做了一系列实验:
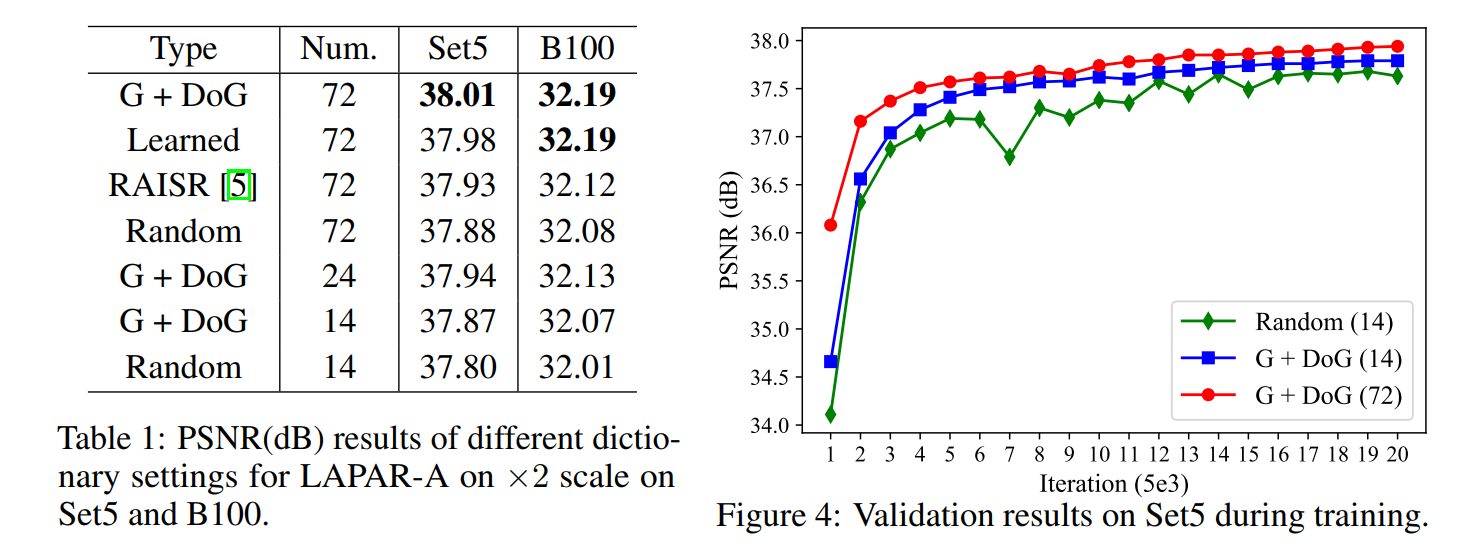
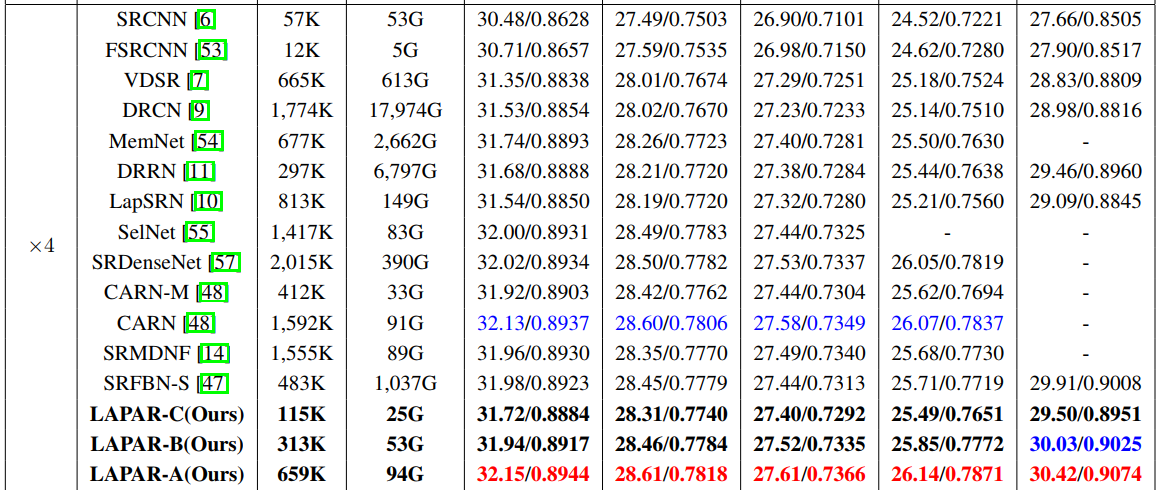
然后是与SOTA方法进行对比:
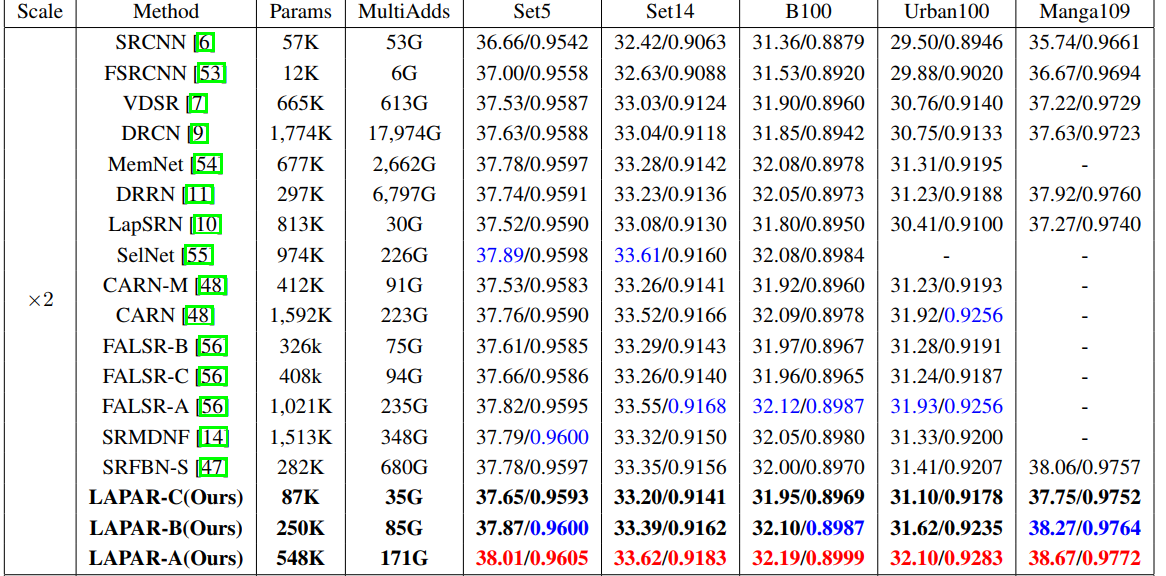
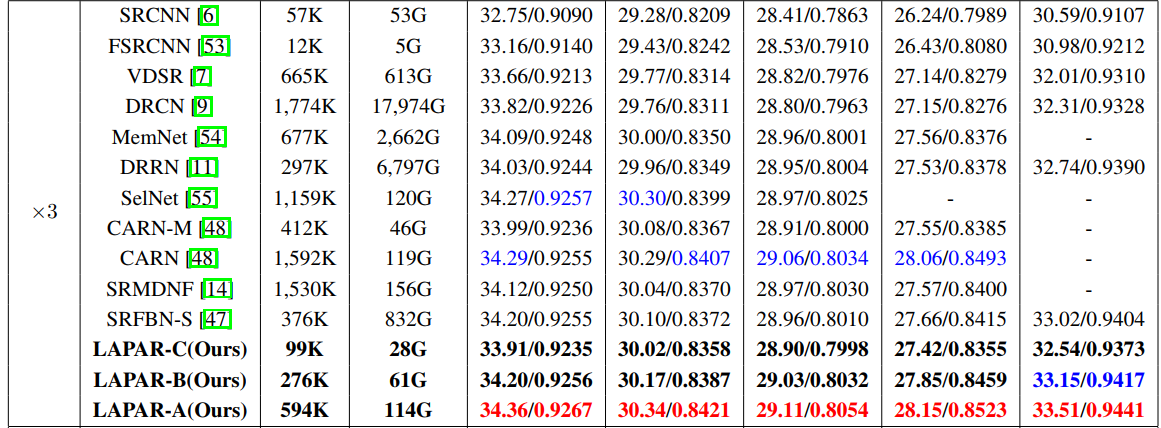
总结与思考
- 这篇工作的角度比较新颖,利用对滤波器空间的线性约束,充当正则项,进而大大减少网络参数和性能消耗
- 只给局部patch使用单独滤波器的使用就意味着,在复原时,放弃了对图像更大范围的特征的直接捕获,转而使用一个卷积网络学滤波器的系数,间接地利用了图像更大范围的特征。感觉颇有Meta-Learning的意味