这篇文章把Transformer应用到low level视觉中,并且把多种low level视觉问题(去噪、超分辨、去雨)放在一起,设计一个预训练模型来统一解决这些问题。
论文背景
图像处理(Image Processing)是计算机视觉系统的底层部分(low level)的一个组成部分。多种图像处理问题都是相关的,自然想到一个基于某个大的数据集预训练(pre-trained)的模型,很可能对其他的图像处理问题有帮助。但是目前几乎没有研究是把预训练模型应用到Image Processing领域的。
预训练模型,一般用于具有以下两个特征的视觉问题:
- 与任务相关的数据量很有限
- 在测试数据输入之前,模型是不知道要完成哪个任务的
而对于图像处理问题来说:
- 问题(1)往往表现在很多数据是私有的/收费的。此外,各种不一致的因素(如相机参数、光照、天气等)也会进一步干扰捕捉到的训练数据的分布。
- 问题(2)表现在,对于不同的图像处理任务,其输入输出形式是有差别的(如超分和去噪的输出尺度就不一样等)
因此,预训练模型应用到图像处理领域是很有价值的。
在CV的high level任务中,AlexNet、VGGNet、ResNet等在ImageNet数据集上训练的模型已经很常用了。而在NLP中,各种基于Transformer的预训练模型也很常见,比如BERT、GPT-3等。
把Transformer引入CV的研究也有很多,但基本都致力于解决图像分类,目标检测等high level任务中。而与这些High level任务不同的是,Image Processing问题的输入和输出都是一幅图像,所以显然不能直接使用他们的预训练模型。
在本工作中,作者提出了一个用于解决Image Process问题的预训练模型,这个模型使用了Transformer的结构,取名为Image Processing Transformer(IPT)。主要框架如下图:
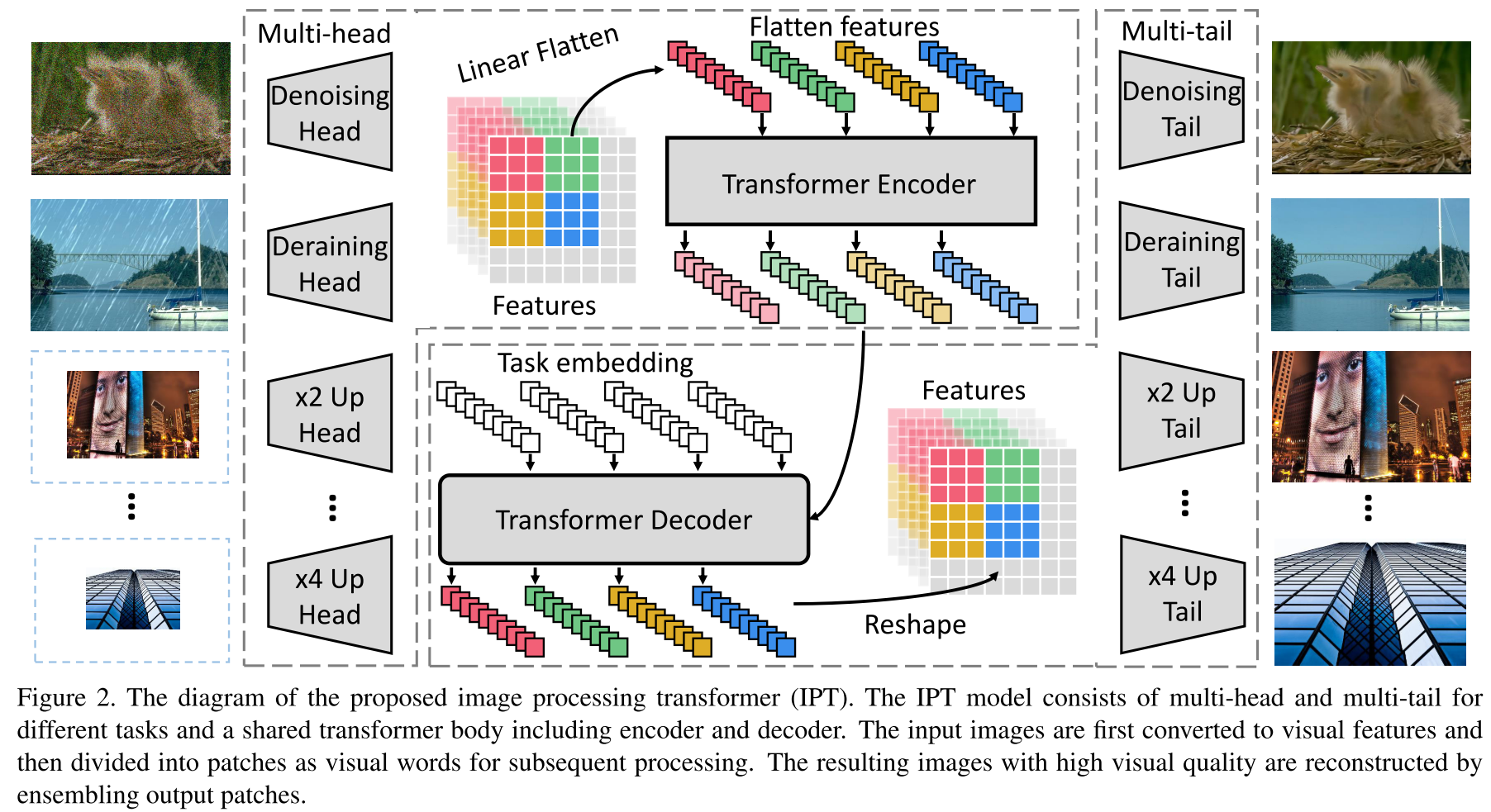
方法详述
IPT的结构
整个结构分为四个部分:Head、Encoder、Decoder、Tail。如上图所示,Encoder、Decoder是公用的,而Head、Tail是任务特异性的。
Head
头部由三个卷积层组成,总的实现\(\mathbb{R}^{3 \times H \times W}\rightarrow \mathbb{R}^{C \times H \times W}\)。
Encoder
把头部提取的特征拆解成一个个patch,每个patch就是一个“word”(类似NLP中的Transformer)。即对于一个特征图\(f_{H} \in \mathbb{R}^{C \times H \times W}\),拆成patch序列\(f_{p_{i}} \in \mathbb{R}^{P^{2} \times C}, i=\{1, \ldots, N\}\),其中\(N=\frac{H W}{P^{2}}\)就是Patch的个数。
另外,如同Transformer中的位置编码,为了维持信息,也设置了位置编码\(E_{p_{i}} \in \mathbb{R}^{P^{2} \times C}\),最后丢进编码器的是\(E_{p_{i}}+f_{p}\)。
编码器的结构就使用了Transformer论文中的结构。编码器的输入尺寸也是\(\mathbb{R}^{P^{2} \times C}\)。总的结构形式化如下: \[ \begin{array}{l} y_{0}=\left[E_{p_{1}}+f_{p_{1}}, E_{p_{2}}+f_{p_{2}}, \ldots, E_{p_{N}}+f_{p_{N}}\right] \\ q_{i}=k_{i}=v_{i}=\mathrm{LN}\left(y_{i-1}\right) \\ y_{i}^{\prime}=\operatorname{MSA}\left(q_{i}, k_{i}, v_{i}\right)+y_{i-1} \\ y_{i}=\operatorname{FFN}\left(\mathrm{LN}\left(y_{i}^{\prime}\right)\right)+y_{i}^{\prime}, \quad i=1, \ldots, l \\ {\left[f_{E_{1}}, f_{E_{2}}, \ldots, f_{E_{N}}\right]=y_{l}} \end{array} \] MSA为传统Transformer模型中的multi-head self-attention模块,FFN包含两个全连接层。
Decoder
Decoder的结构也类似: \[ \begin{array}{l} z_{0}=\left[f_{E_{1}}, f_{E_{2}}, \ldots, f_{E_{N}}\right] \\ q_{i}=k_{i}=\mathrm{LN}\left(z_{i-1}\right)+E_{t}, v_{i}=\mathrm{LN}\left(z_{i-1}\right) \\ z_{i}^{\prime}=\operatorname{MSA}\left(q_{i}, k_{i}, v_{i}\right)+z_{i-1} \\ q_{i}^{\prime}=\mathrm{LN}\left(z_{i}^{\prime}\right)+E_{t}, k_{i}^{\prime}=v_{i}^{\prime}=\mathrm{LN}\left(z_{0}\right) \\ z_{i}^{\prime \prime}=\operatorname{MSA}\left(q_{i}^{\prime}, k_{i}^{\prime}, v_{i}^{\prime}\right)+z_{i}^{\prime} \\ z_{i}=\mathrm{FFN}\left(\mathrm{LN}\left(z_{i}^{\prime \prime}\right)\right)+z_{i}^{\prime \prime}, \\ {\left[f_{D_{1}}, f_{D_{2}}, \ldots, f_{D_{N}}\right]=y_{l}} \end{array} \]
Tail
尾部的结构按照任务的不同有差异。超分辨模型则有一个上采样的操作。
在ImageNet数据集上的预训练
在训练中,作者引入了两种学习的方式,一种是经典的图像恢复中的监督学习;另一个称为对比学习(contrastive learning)。
监督学习
基本操作就是把ImageNet数据集中的各种语义信息全部去除,针对不同的Image Processing问题,使用不同的退化模型构造成对数据集:SR使用双三次退化;denoising加高斯噪声等。
整个过程形式化如下: \[ \begin{array}{l} I_{\text {corrupted}}=\boldsymbol{f}\left(I_{\text {clean}}\right)\\ \mathcal{L}_{\text {supervised}}=\sum_{i=1}^{N_{t}} L_{1}\left(\operatorname{IPT}\left(I_{\text {corrupted}}^{i}\right), I_{\text {clean}}\right) \end{array} \] 具体实现过程中,对于每一个Batch,随机选择一个图像处理task(如SR、denoising、deraining)对应的成对数据集进行训练。
对比学习
由于IPT模型要用于多个任务,所以为了强化它的泛化能力,引入对比学习,从而引入不同图像的不同patch之间的关系信息。例如,从相同的特征图中裁剪出来的patch更有可能聚在一起,它们更应该被嵌入到相似的位置中。
形式化地,对于每张图\(x_j\),它所在的Batch为\(X=\left\{x_{1}, x_{2}, \ldots, x_{B}\right\}\),其Decode的结果为\(f_{D_{i}}^{j} \in \mathbb{R}^{P^{2} \times C}, i=\{1, \ldots, N\}\)。目标是最小化来自同一幅图像的patch之间的距离,最大化来自不同图像的patch之间的距离。所以引入如下损失: \[ \begin{array}{r} l\left(f_{D_{i_{1}}}^{j}, f_{D_{i_{2}}}^{j}\right)=-\log \frac{\exp \left(d\left(f_{D_{i_{1}}}^{j}, f_{D_{i_{2}}}^{j}\right)\right)}{\sum_{k=1}^{B} \mathbb{I}_{k \neq j} \exp \left(d\left(f_{D_{i_{1}}}^{j}, f_{D_{i_{2}}}^{k}\right)\right)} \\ \mathcal{L}_{\text {constrastive}}=\frac{1}{B N^{2}} \sum_{i_{1}=1}^{N} \sum_{i_{2}=1}^{N} \sum_{j=1}^{B} l\left(f_{D_{i_{1}}}^{j}, f_{D_{i_{2}}}^{j}\right) \end{array} \] 其中\(d(\cdot,\cdot)\)为余弦相似度\(d(a, b)=\frac{a^{T} b}{\|a\|\|b\|}\)。
最终的loss为: \[ \mathcal{L}_{I P T}=\lambda \cdot \mathcal{L}_{\text {contrastive}}+\mathcal{L}_{\text {supervised}} \]
实验结果

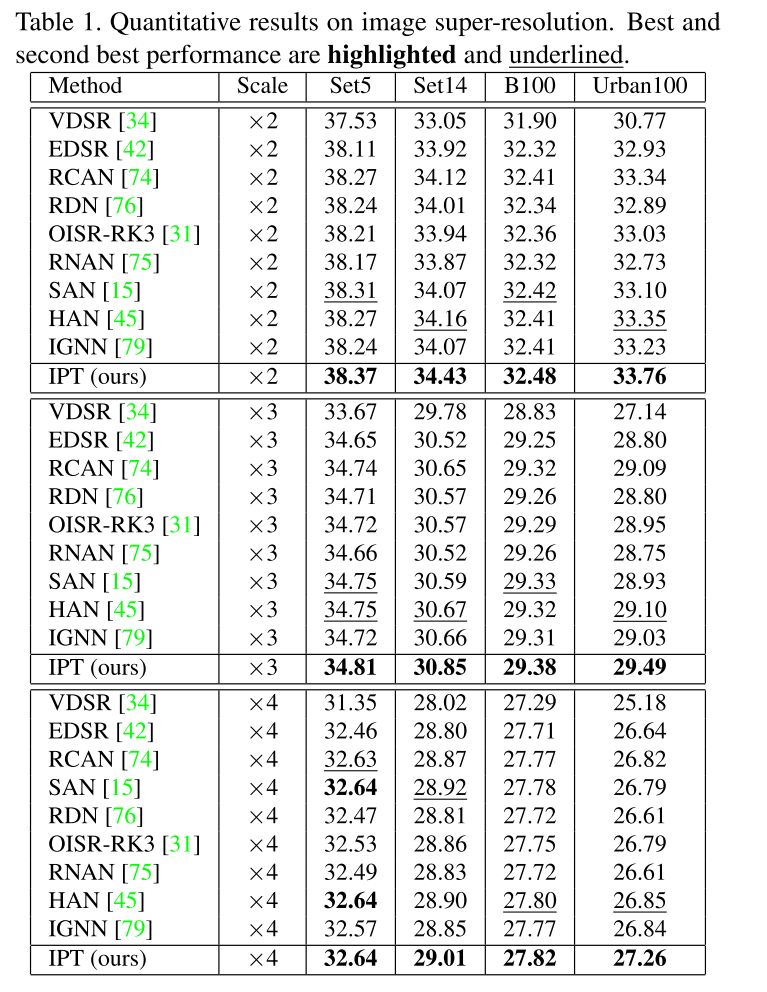
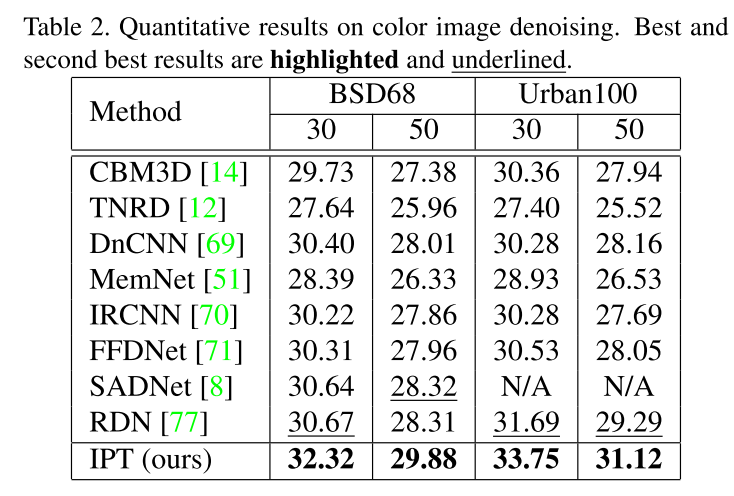
在各个任务上都达到了SOTA:

总结与思考
利用Transformer的强大表示能力+ImageNet的海量数据,作者成功达到的多个low level问题的SOTA,真的很吃惊,虽然源码没有放出来,但是放出来也很难复现整个训练过程(32张V100.。。)
作者给Transformer+low level挖了个新坑,读这篇文章让我系统性的学了一下Transformer相关的内容,这是我之前忽视的知识,感觉还是挺有收获的