简述
本文提出的方法要完成的任务是在超低分辨率下的超分辨,正视超分辨的ill-posed属性,从一张LR图像中恢复出多张可能的HR图像。这个方法被作者称为VarSR。
主要思路是:通过最小化在HR与LR的KL散度来连接LR图像与HR图像间的表示能力,从而把LR图像和HR图像同时encode到同一个隐变量特征空间。然后SR模块的输入是这个隐变量,生成一个与Ground-truth HR之间的像素/感知上的相似的SR结果。由于HR图像的多样性程度高于LR图像,因此HR图像的潜在变量要比LR图像密集得多。所以在推理过程中,从隐变量空间中多次取样,从而产生多种SR图像。整个过程如下图所示。
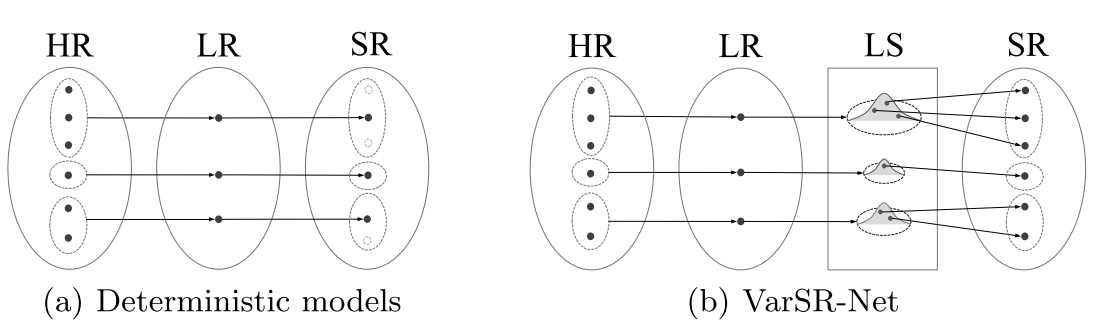
方法详述
整体框架描述
传统的SR框架都是这样的: \[ \hat{I}_{H}=g_{S R}\left(I_{L}\right) \] 使用SR图片\(\hat{I}_{H}\)与真实HR图像\(I_{H}\)之间的重构损失、感知损失、对抗损失训练。但是,由于\(I_{H}\)的详细信息难以在\(I_{L}\)中编码,使得超分辨率模型无法推断出可靠的输出,特别是对于极低分辨率的输入。
为了解决这个问题,本文引入了一个隐变量,作为SR子模块的输入,描述\(I_{H}\)的信息,处理\(I_{L}\)的模糊性: \[ \hat{I}_{H}=g_{S R}\left(I_{L}, E_{H}\left(I_{H}\right)\right) \] 其中,\(E_{H}(\cdot)\)为一个encoder,用于从\(I_H\)中提取特征。而SR模型\(g_{SR}\)不仅输入低分辨图像\(I_L\)中获取信息,也从encoder编码的\(I_H\)的特征中获取信息,从而做出更准确的超分。
然而,(2)式中,需要获得\(I_H\)的信息,这在超分中显然是不妥当的。所以我们需要只从\(I_L\)中去估计\(E_{H}(\cdot)\)。
因此,作者为\(I_L\)引入另一个encoder \(E_L(\cdot)\)。由于SR问题的ill-posed属性,一张LR图像对应多张HR图像,因此,确定性的encoder是不够的。这里作者把隐变量的空间建模成一个多变量的高斯分布,这样就能从分布中多次采样,从而提供一个如下的“一对多”的映射: \[ E_{L}(x)=\left[\mu_{x}, \sigma_{x}\right] \text { and } E_{H}(x)=\left[\mu_{x}, \sigma_{x}\right] \] 其中\(x\)代表HR或者LR图像,而\(\mu_x\)与\(\sigma_x\)分别是分布的期望和方差。
于是,作者的关键idea就是,让两个隐变量 \(E_L(\cdot)\)和 \(E_H(\cdot)\)的分布对应起来。换句话说,就是要使得从 \(E_L(\cdot)\)中取样和从 \(E_H(\cdot)\)是高度相似的。因此,作者使用$E_{H}(I_{H}) \(和\) E_{L}(I_{L})$两个分布之间的KL散度来训练这两个encoder。
测试与训练过程描述如下
在训练过程中,超分网络\(G(\cdot, \cdot)\)的输入\((I_L, z)\),其中\(z\)是从HR图片的encoder对应的高斯分布\(\mathcal{N}\left(E_{H}^{\mu}\left(I_{H}\right), E_{H}^{\sigma}\left(I_{H}\right)\right)\)中取样(因为HR图像在训练过程中是可以得到的)。
而在测试过程中,超分网络\(G(\cdot, \cdot)\)的输入\((I_L, z)\),其中\(z\)是从LR图片的encoder对应的高斯分布\(\mathcal{N}\left(E_{L}^{\mu}\left(I_{L}\right), E_{L}^{\sigma}\left(I_{L}\right)\right)\)中取样。即,从一幅LR图片\(I_L\)获得多种HR图片\(\left\{\hat{I}_{H}^{1}, \ldots, \hat{I}_{H}^{n}\right\}\)的方法如下: \[ \hat{I}_{H}^{i}=G\left(I_{L}, z_{i}\right), \quad z_{i} \sim \mathcal{N}\left(E_{L}^{\mu}\left(I_{L}\right), E_{L}^{\sigma}\left(I_{L}\right)\right) \]
与条件变分自编码器(cVAEs)的关系
cVAE是用来估计一个条件分布\(p_{\theta}(x \mid y)\)的,其中\(x\)为数据,\(y\)为条件。给定条件\(y\),则\(z\)从一个先验分布\(p_\theta(z|y)\)中取。而\(x\)是从分布\(p_\theta(x|y,z)\)中取的(感觉这里都用\(\theta\)是不是不太妥?)。而\(x\)的多样性\(\left\{x_{i}\right\}\)由多个隐变量\(\left\{z_{i}\right\}\)来产生。cVAE的evidence lower bound(ELBO)如下: \[ \begin{aligned} L_{C V A E}(x, y ; \theta, \phi) &=\mathbb{E}_{q_{\phi}(z \mid x, y)} \log p_{\theta}(x \mid y, z) \\ &-D_{K L}\left(q_{\phi}(z \mid x, y) \| p_{\theta}(z \mid y)\right) \leq \log p_{\theta}(x \mid y) \end{aligned} \] 上面的式子利用Jensen不等式很容易推出来,其中\(q_{\phi}(z|x, y)\)是对真实后验概率\(p_\theta(z|y)\)的估计(为啥前面又说是先验?)。根据变分推断的思想,最大化这个下界,即可最大化似然函数\(\log {p_\theta(x|y)}\)。
如果我们假设:高分辨图像包含了其对应的低分辨图像的所有信息。那么,我们能将VarSR模型翻译为一个cVAE的结构,\(x\)就是高分辨图像\(I_H\),\(y\)为低分辨图像\(I_L\),\(p_\theta(z|y)\)就是LR encoder\(E_{L}\left(I_{L}\right)\),\(q_{\phi}(z \mid x, y)\)是HR encoder\(E_{H}\left(I_{H}\right)\),\(p_{\theta}(x|y, z)\)为超分网络\(G\left(I_{L}, z\right)\)。而\(\log p_{\theta}(x \mid y, z)\)这项,其实就是使用像素级别的重构/感知等损失。作者表示,这种解释为VarSR模型提供了理论支持,也就是使观察数据的条件对数似然最大化。
目标函数
损失函数主要为三个:
像素级别的重构损失:用于鼓励HR编码器\(E_H(\cdot)\)提取高分辨率图像的信息特征 \[ \mathcal{L}_{\mathrm{pixel}}=\frac{1}{r^{2} H W} \sum_{x=1}^{r H} \sum_{y=1}^{r W}\left(I_{H}^{x, y}-G\left(I_{L}, z\right)^{x, y}\right)^{2}, z \sim \mathcal{N}\left(E_{H}^{\mu}\left(I_{H}\right), E_{H}^{\sigma}\left(I_{H}\right)\right) \]
KL散度:最小化LR图像与HR图像在隐变量空间的分布差距 \[ \mathcal{L}_{\mathrm{KL}}=D_{K L}\left(q\left(z \mid I_{H}\right) \| p\left(z \mid I_{L}\right)\right) \]
对抗损失:用于恢复更真实的纹理 \[ \mathcal{L}_{\mathrm{adv}}=\underset{\hat{I} \sim \mathbb{P}_{g}}{\mathbb{E}}[D(\hat{I})]-\underset{I \sim \mathbb{P}_{r}}{\mathbb{E}}[D(I)]+\delta \underset{\hat{I} \sim \mathbb{P}_{\hat{\jmath}}}{\mathbb{E}}\left[\left(\left\|\nabla_{\hat{I}} D(\hat{I})\right\|_{2}-1\right)^{2}\right] \]
总损失是三者的加权和: \[ \mathcal{L}=\lambda_{\text {pixel }} \mathcal{L}_{\text {pixel }}+\lambda_{\mathrm{KL}} \mathcal{L}_{\mathrm{KL}}+\lambda_{\mathrm{adv}} \mathcal{L}_{\mathrm{adv}} \]
实验
作者在两个数据集上做了实验,一个是人脸数据集,一个是数字数据集。选择的比较对象有:
- PRSR:像素递归的超分辨方法(但是由于人脸数据集的像素为64x64,对于PRSR来说代价太大,因此PRSR没有在人脸数据集上面测。)
- MR-GAN:使用了基于动量的损失来代替均方误差,从而降低在cGAN中的模式坍塌
此外,SRGAN作为deterministic SR technique(就是一张LR,只产生一张SR的技术)的baseline。对于数字数据集,由于数字数据集输入的低分辨率图像具有极低的维数,例如2×4像素,因此我们对整个方法使用带有跳跃连接的自动编码器。因此,后文中将deterministic SR technique表示为“Det”,而不是“SRGAN”。
数据集
- 人脸数据集采用CelebA。一共200k张,100k作为训练集,1k作为测试集。HR分辨率为64x64,LR分辨率为8x8。对于网络结构来说,为了公平期间,和MR-GAN中设置的一样,都是8个Res Block。
- 数字数据集用了两个:
- MNIST。60k张训练集,10k张测试集。HR分辨率为64x64,LR分辨率为8x8。
- LP。110k训练,7k测试。
评价指标
由于VarSR-Net不是用来生成确定性结果的。因此作者根据不同超分辨图像的平均值/最佳分数来进行评估。
- 传统的PSNR、SSIM、MSE
- 对于数字数据集,使用图像分类方法,来衡量语义上的可信性
- 对于人脸数据集,使用感知图像质量指标(具体使用了LPIPS分数、人脸验证网络FaceNet提取的特征间的距离)
此外,为了衡量生成的图像的多样性,我们使用了结果SR图像之间的平均LPIPS距离来衡量。
定性结果
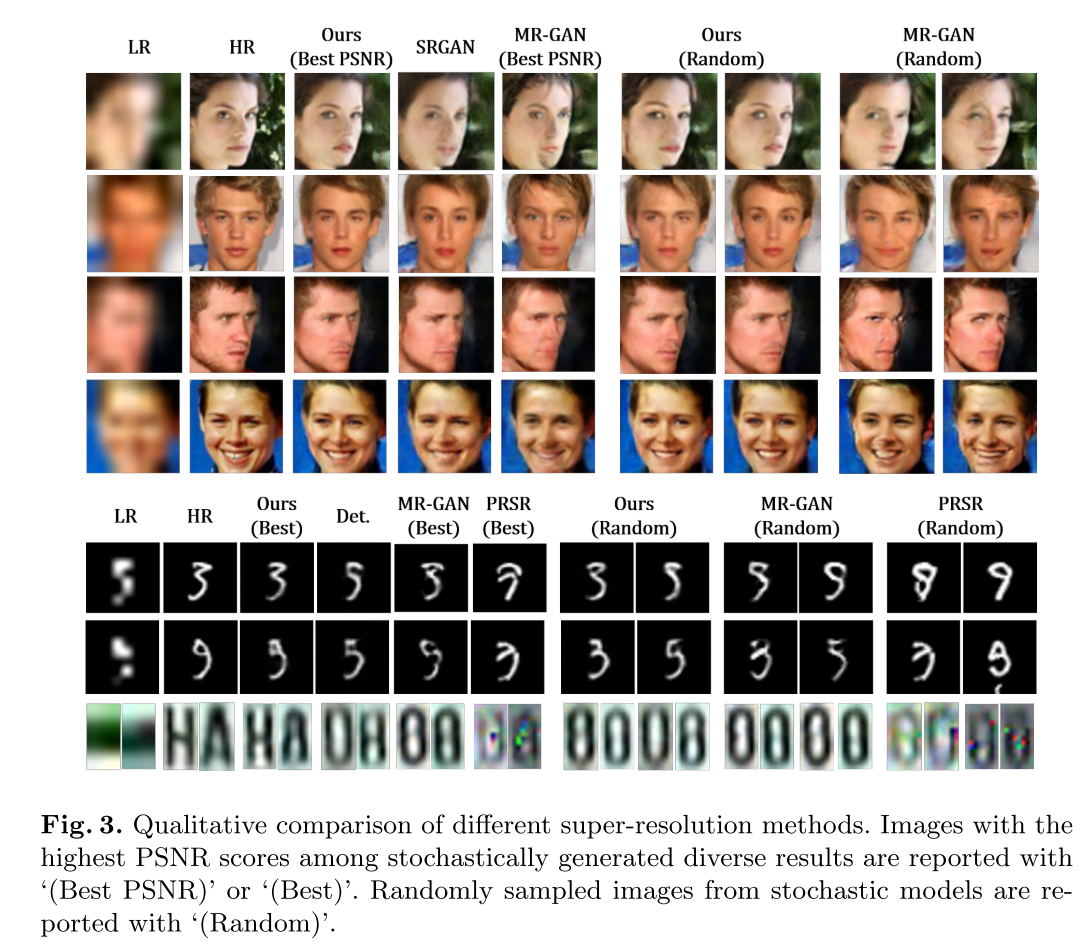
另外,作者还尝试了其他High level的任务,如人脸属性编辑、属性迁移等,也取得了不错的效果:

定量结果
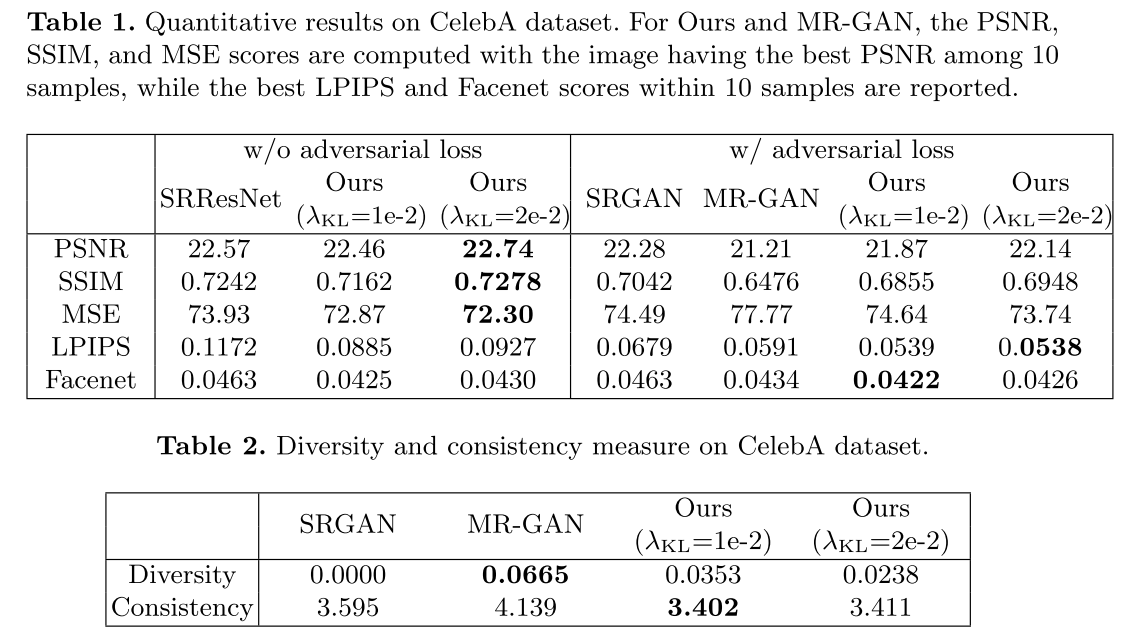
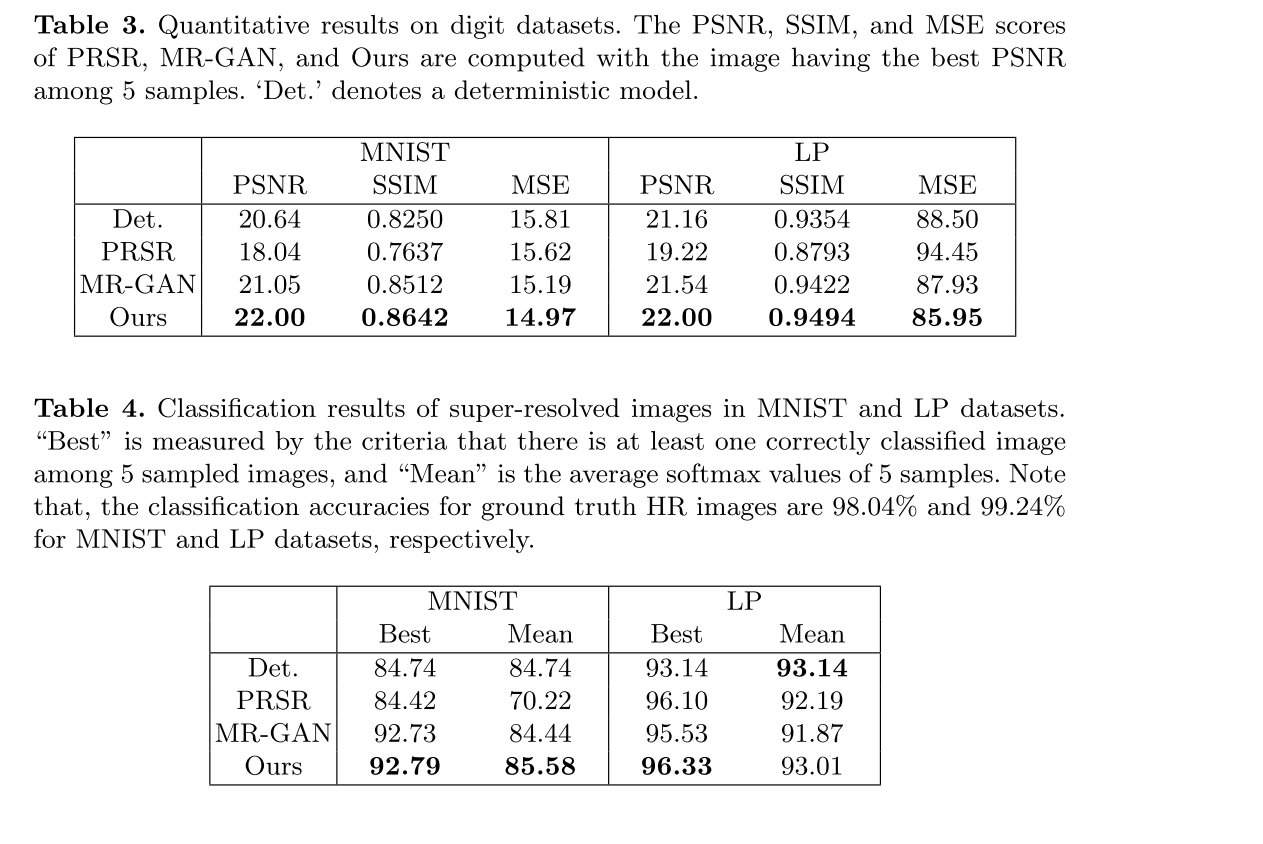
总结与思考
- 这篇文章主要是用了cVAE的思想来解决SR的ill-posed问题,但是讲故事很有水平,一开始先重点讲HR encoder和LR encoder,把读者代入这种latent space的思路后,话锋一转,引入与cVAE关系,一下子就引入了可解释性。
- 但是仔细看这篇文章的实验设计,还是能学到很多。相关的评价标准,以及baseline的选择都很巧妙。由于我的可逆网络毕设,也是解决SR的ill-posed问题,所以本文的实验设计很有参考价值。