论文背景
RealNVP的全称,real-valued non-volume preserving ,可以翻译为“真实值非体积保持”。对于无监督学习来说,感兴趣的数据通常是高维的、高度结构化的,因此该领域的挑战是构建足够强大的模型,以捕获其复杂性,但仍然是可训练的。作者通过引入实值非体积保持(real NVP)转换来解决这一挑战,这是一种易于处理但表现能力强的高维数据建模方法。
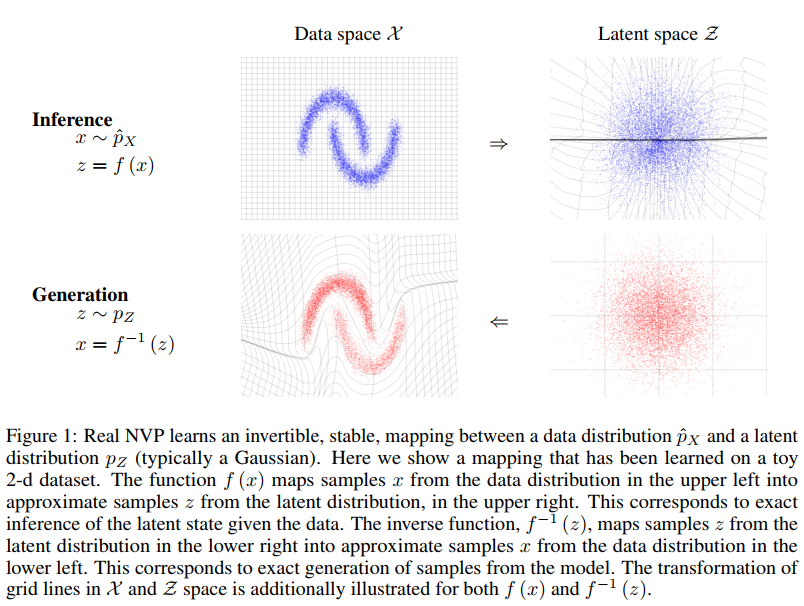
基本思想是把数据空间映射到隐空间z,如上图所示。
以前的相关工作:
- 受限玻尔兹曼机、深度玻尔兹曼机
- 通过利用两方的条件独立性来训练模型结构,可以对潜在变量进行有效的精确或近似后验推断。然而,由于潜在变量的相关边际分布的难处理性。训练、评估和抽样程序必须使用Mean Field inference 和马尔可夫链蒙特卡洛法。对于此类复杂模型,收敛时间往往是不确定的。另外,各种近似也限制了其性能
- 有向概率图模型
- 在推理过程中的各种近似,限制了性能
- 自回归模型
- 避免引入隐变量,从而消除各种近似。
- RNN、LSTM
- 非并行,慢
- GAN
- 度量生成样本的多样性的指标不明确
- 训练不稳定
而作者提出的方法,可以训练这样一个生成网络\(g\),它将潜在变量\(z \sim p_Z\)映射到样本\(x \sim p_{X}\),理论上不需要像GANs那样使用鉴别器网络,也不需要像变分自编码器那样使用近似推理。的确,如果g是双射,可以利用变量的变化公式,通过极大似然对其进行训练: \[ p_{X}(x)=p_{Z}(z)\left|\operatorname{det}\left(\frac{\partial g(z)}{\partial z^{T}}\right)\right|^{-1} \]
主要方法
上周读的NICE,也是这个作者之前的工作,作者表示,自己在NICE的基础上,定义了一个更强大的双射函数类,它支持精确和可处理的概率密度评估与推理。代价函数不依赖于固定的形式重构代价(比如L2损失等),因此可以产生更加非平滑的样本。另外,这次提出的方法可以使用batch normalization、ResBlock等,从而构建一个具有多个抽象层次的深度多尺度架构(a very deep multi-scale architecture with multiple levels of abstraction)。
耦合层
Real NVP的耦合层相较于NICE的有很大的不同:
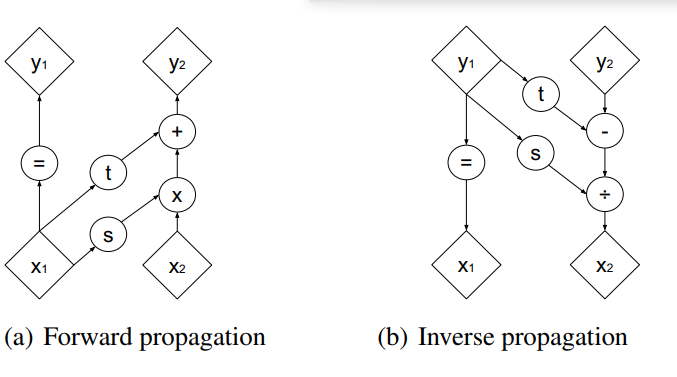
写成式子: \[ \begin{aligned} \left\{\begin{array}{l} y_{1: d}=x_{1: d} \\ y_{d+1: D}=x_{1: 1: D} \odot \exp \left(s\left(x_{1: d}\right)\right)+t\left(x_{1: d}\right) \end{array}\right.\\ \Leftrightarrow\left\{\begin{array}{l} x_{1: d}=y_{1: d} \\ x_{d+1: D}=\left(y_{d+1: D}-t\left(y_{1: d}\right)\right) \odot \exp \left(-s\left(y_{1: d}\right)\right) \end{array}\right. \end{aligned} \]
与NICE同理,其雅克比行列式也是易于计算的: \[ \frac{\partial y}{\partial x^{T}}=\left[\begin{array}{cc} \mathbb{I}_{d} & 0 \\ \frac{\partial y_{d+1: D}}{\partial x_{1: d}^{T}} & \operatorname{diag}\left(\exp \left[s\left(x_{1: d}\right)\right]\right) \end{array}\right]=\exp \left[\sum_{j} s\left(x_{1: d}\right)_{j}\right] \] 计算耦合层的逆并不需要计算s或t的逆,因此这些函数可以任意复杂且难以求逆。
Mask Convolution
另外,在实际实现中,可以使用一个Masked convolution,即使用一个二值化的mask \(b\): \[ y=b \odot x+(1-b) \odot(x \odot \exp (s(b \odot x))+t(b \odot x)) \] 对于mask,有以下两种模式:
- 棋盘格掩蔽(checkerboard masking)
- 通道掩蔽(channel-wise masking)
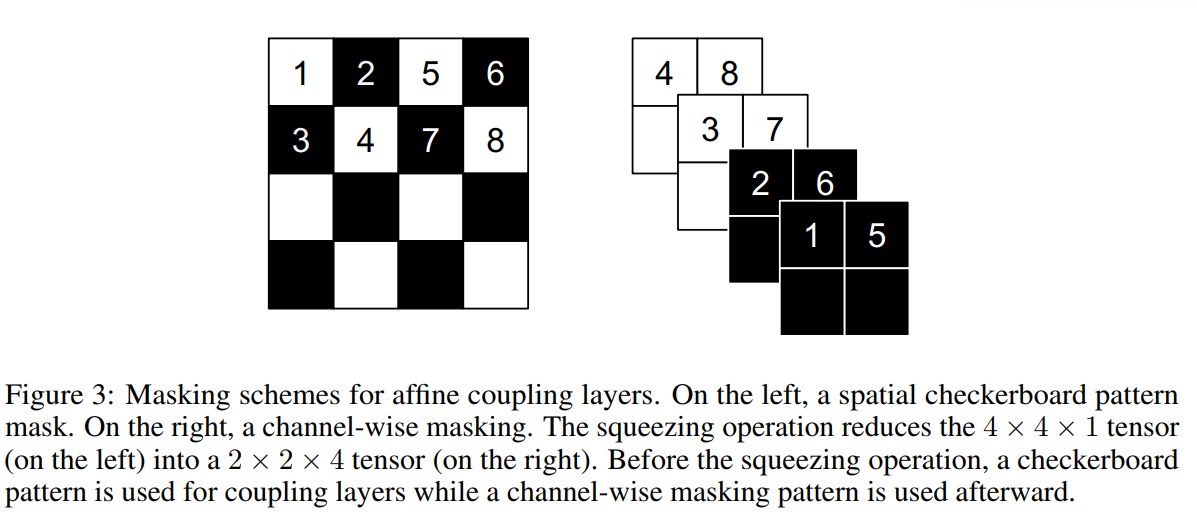
耦合层的整合
尽管耦合层功能强大,但它们的前向转换保留了一些组件(比如\(x_{1: d}\))。可以通过将耦合层组合为交替模式来克服这一困难,这样,在一个耦合层中保持不变的组件,将在下一个耦合层中更新:
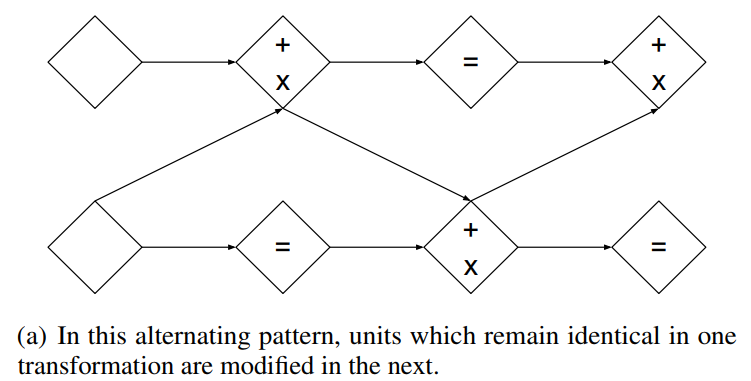
另外,多个耦合层的雅克比行列式只需累乘即可: \[ \begin{aligned} \frac{\partial\left(f_{b} \circ f_{a}\right)}{\partial x_{a}^{T}}\left(x_{a}\right) &=\frac{\partial f_{a}}{\partial x_{a}^{T}}\left(x_{a}\right) \cdot \frac{\partial f_{b}}{\partial x_{b}^{T}}\left(x_{b}=f_{a}\left(x_{a}\right)\right) \\ \operatorname{det}(A \cdot B) &=\operatorname{det}(A) \operatorname{det}(B) \end{aligned} \]
多尺度结构(Multi-scale architecture)
(这一部分我看的不是很懂)
作者通过squeeze操作实现了一个多尺度的架构:对于每个通道,将图像分割成形状为2×2×c的子正方形,然后将其重新塑形为形状为1×1×4c的子正方形。squeeze操作将一个s×s×c张量转化为一个2s×2s×4c张量,有效地交换了通道数与空间大小的关系。
在每个尺度上,将几个操作组合成如下序列:我们首先应用三个耦合层,交替使用checkerboard masking,然后执行squeeze操作,最后应用三个耦合层,交替使用channel-wise masking。
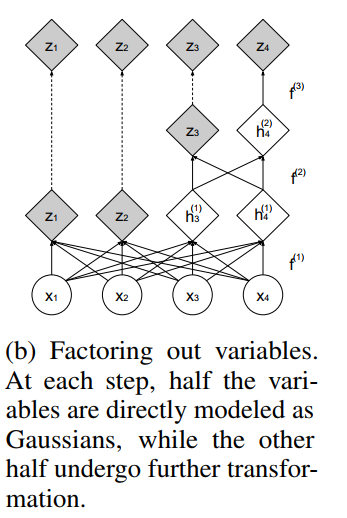
在所有耦合层中传播一个D维向量将是很麻烦的,因为计算和内存成本,以及需要训练的参数的数量。由于这个原因,作者遵循VGG中的设计选择,并定期提出一半的尺寸:
Batch normalization
批处理归一化的影响很容易包含在雅可比矩阵的计算中,因为它是对每个维度的线性调整。也就是说,给定估计的批处理统计量: \[ x \mapsto \frac{x-\tilde{\mu}}{\sqrt{\tilde{\sigma}^{2}+\epsilon}} \] 我们具有雅克比矩阵: \[ \left(\prod_{i}\left(\tilde{\sigma}_{i}^{2}+\epsilon\right)\right)^{-\frac{1}{2}} \]
实验结果

总结与思考
这篇是作者在本人的NICE工作的基础上的一篇完善工作,主要进步在于:
改善了仿射层的结构
使用了mask卷积保证了推理过程中所有信息都被处理
考虑了多尺度的结构
RealNVP 的雅可比行列式不再恒等于 1,行列式的几何意义就是体积,所以行列式等于 1 就意味着体积没有变化,而仿射耦合层的行列式不等于 1 就意味着体积有所变化,所谓“非体积保持”。
第一篇 NICE 中,作者提出了加性耦合层。后面也提到了乘性耦合层,只不过没有用上;而在 RealNVP 中,加性和乘性耦合层结合在一起,成为一个一般的“仿射耦合层”。
本文的mask卷积实质上就是对两个耦合层直接的信息实施一种可逆的打乱,比NICE中的单纯交换分区中两个子集的角色的做法要更优