这篇文章也是INN系列的论文中经常引用的一篇文章,只在arxiv上看到,貌似没有被哪个会议接收,读下来确实发现idea的创新性不是特别足。但是发现其introduction中的对生成模型的归纳还是挺到位的,所以学习学习。
论文背景
作者回顾了几个典型的条件生成模型的缺点:
- cGAN:训练不够稳定,容易模式坍塌
- cVAE:L2 loss的引入,使得生成的图像比较模糊
但是可逆神经网络(INN)就可以克服上述的一些问题,利用双向传递、雅克比行列式易于计算的特点,建立一个“待生成的分布”与一个“易于取样的潜在分布”之间的双向映射。在训练过程中,待生成的分布\(p(\mathbf x)\)的最大似然在隐空间中优化(这样看来,那篇Analyzing Inverse Problems其实用的不只是隐空间中优化);而在推理过程中,隐变量\(\mathbf z\)即可逆向映射到待生成的数据。
对于非条件的INN来说,看上去和VAE的方法很一致,但是值得注意的是,他克服了VAE方法的好几个弱点:
- 不再需要L2 重构损失,避免了图像模糊
- 每一个\(\mathbf x\)都映射到一个唯一的\(\mathbf z\),所以并不再需要后验概率\(p(\mathbf z|\mathbf x)\)了,这样就避免了VAE中各个样本的潜空间区域不相交或重叠的问题
在训练稳定性和样本多样性方面,INN表现出与VAE架构相同的优势,但具有更加优越的图像质量。
但是同时,INN也有一些相较于传统神经网络的缺失之处,比如池化层、Batch normalization层等(这句话我存疑,感觉是作者为了批判而批判,明明那个affine coupling block中的网络部分并不需要可逆,凭啥不能加池化或者BN呢)。
于是作者声称提出了一个新的网络结构——cINN(条件可逆神经网络)。
方法详述
网络结构
我觉得其实这篇工作的亮点乏善可陈,用下面这一张图就可以概括:

仿射耦合层的结构,与我的另一篇阅读Analyzing Inverse Problems中的结构并无差别,只不过在两个不可逆的子网络的输入处,连接上条件特征。
训练过程
训练过程主要就是最大化似然概率(MAXIMUM LIKELIHOOD TRAINING)。具体就是,首先\(\mathbf x\)域的样本是已知的,在\(\mathbf x\)域中采样,\(\mathbf z\)域的概率密度函数是已知的,利用利用易于计算的雅克比行列式,使用以下公式可以表示出,\(\mathbf x\)域中的样本的出现概率: \[ p_{X}(\mathbf{x} ; \mathbf{c}, \theta)=p_{Z}(f(\mathbf{x} ; \mathbf{c}, \theta))\left|\operatorname{det}\left(\frac{\partial f}{\partial \mathbf{x}}\right)\right| \] 又因为似然概率\(p(\theta ; \mathbf{x}, \mathbf{c}) \propto p_{X}(\mathbf{x} ; \mathbf{c}, \theta) \cdot p_{\theta}(\theta)\),因此,取负对数后,损失函数如下: \[ \mathcal{L}=\mathbb{E}_{i}\left[-\log \left(p_{X}\left(\mathbf{x}_{i} ; \mathbf{c}_{i}, \theta\right)\right)\right]-\log \left(p_{\theta}(\theta)\right) \] 把(1)式代入,\(p_Z()\)利用标准高斯分布代入,而对\(\theta\)的先验也看做高斯,则可以得到: \[ \mathcal{L}=\mathbb{E}_{i}\left[\frac{\left\|f\left(\mathbf{x}_{i} ; \mathbf{c}_{i}, \theta\right)\right\|_{2}^{2}}{2}-\log \left|J_{i}\right|\right]+\tau\|\theta\|_{2}^{2} \]
某些重要的细节部分
通道随机排列:在每个仿射耦合层之间,使用随机正交矩阵实现通道的随机排列,这使得耦合块中的两个信息流之间有更多的交互。矩阵在整个训练过程中都是固定的,并且保证它是可逆的。
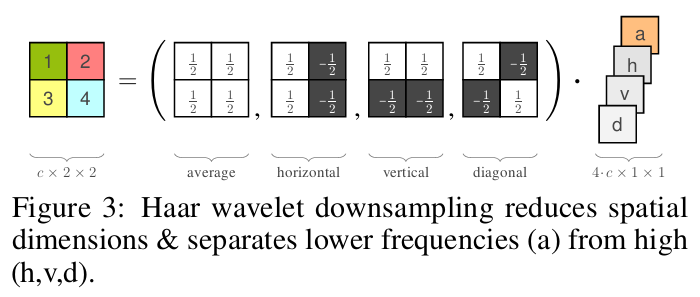
哈尔小波变换:相比于先前的INN都用到的棋牌格式的下采样方式,作者发现使用哈尔小波变换比较适合。本质上是将图像分解为平均、垂直、水平和对角四个特征通道。垂直、水平和对角这三个导数通道包含了高分辨率的信息,我们可以在早期分离掉这些信息,在cINN的后期将剩余的信息进一步转化。Haar wavelet也能用作在中间混合不同流的信息,可以看做是对上述的通道随机排列的补充。
实验结果
作者主要拿这个模块做了两个实验,一个是条件生成MNIST、另一个是图像上色。两个网络结构如下:
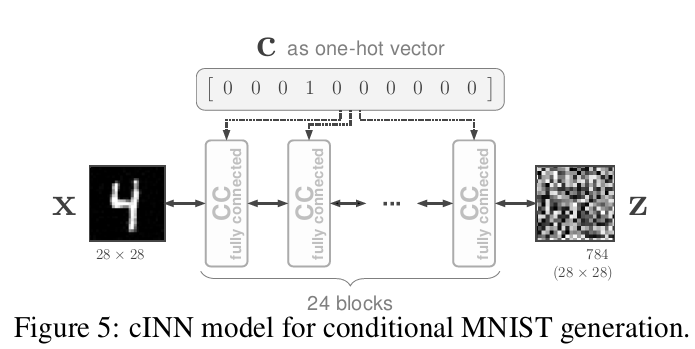
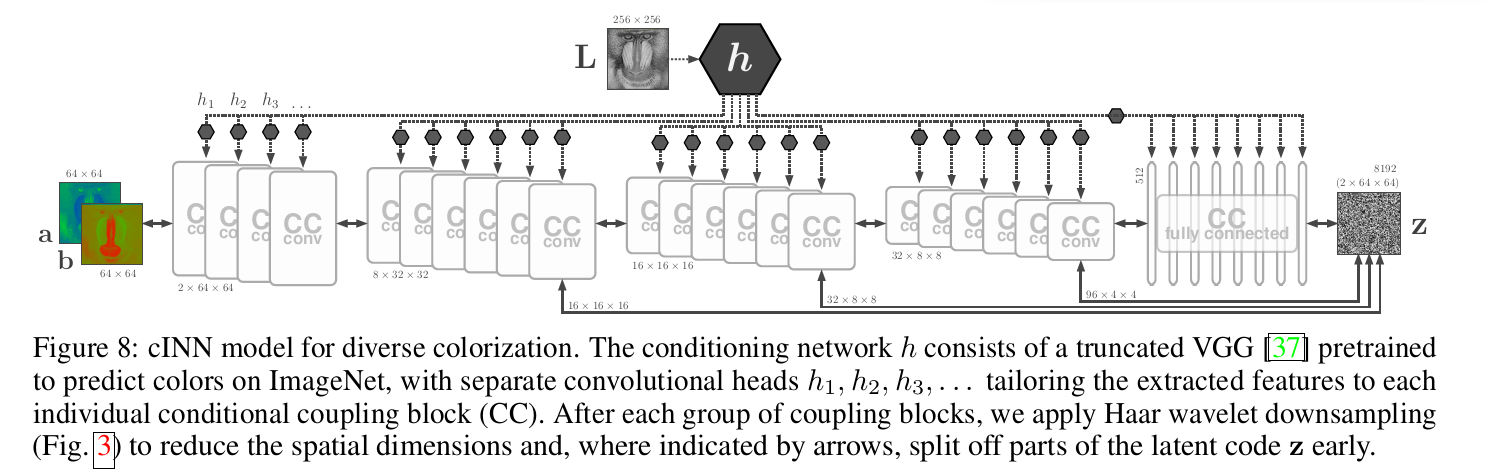
CC conv代表条件仿射耦合层的子网络s和t用的是卷积层。而CC fully connected是用的全连接层。
MINST的结果如下:

使用PCA在z域上找主轴,可以发现不同轴上控制的不同的特征:

总结与思考
- 在阅读这篇的时候,我把cGAN与cVAE的特点又重新的理解了一篇,收获颇丰。cGAN不易造成模糊,但容易出现模型坍塌,且训练不稳定;cVAE使用了L2重构,造成图像模糊。
- 对于INN体系的训练方式来说,Analyzing Inverse Problems那篇的使用的是MMD(最大均值差异)方法,不需要显示的计算雅克比行列式,所以模型的重点在于保证双向传播的高效性,直接在样本上进行MMD最小化;而本文使用的是最大似然,需要显式地计算雅克比矩阵。我觉得最大似然的可解释性更强,但是在Invertible Image Rescaling中也没有使用最大似然的训练方法,而是把Analyzing Inverse Problems的MMD改成了JS散度。
- 另外,相对于Invertible Image Rescaling和Analyzing Inverse Problems把“条件”也放在网络中进行可逆的传播,本文是粗暴地将其插入INN的不可逆模块中。难怪在Invertible Image Rescaling中作者表示,这篇文章“x和z之间的可逆建模以y为条件,在给定x时模型不能生成y,因此不适用于图像的缩放任务”其实是有道理的。