论文背景
作者表示,SR问题本来就是一个ill-posed的问题,可是大多数工作忽略了这一点,只致力于去学一个单图像到单图像的映射。而作者利用了基于标准化流(Normalizing Flow)的方法,去学一个LR到HR分布的映射(学习与输入LR图像相对应的真实HR图像的分布,即可以看做是给定LR图像,HR的条件概率分布),同时还表明在去噪、复原的任务中也能发挥作用。
所谓标准化流(Normalizing Flow)的方法,是用来拟合一些复杂概率分布的。实际上就是学一个可逆神经网络\(f_{\theta}\),使用它的逆过程\(f_{\theta}^{- 1}\)把一个简单的分布(比如高斯分布、均匀分布等)\(p_{\mathbf{z}}(\mathbf{z})\)变成\(\mathbf{y} = f_{\theta}^{- 1}(\mathbf{z})\)。
主要方法
SR中的条件标准化流
设\(\mathbf{x}\)是LR图像,\(\mathbf{y}\)是HR图像。本文要求确定LR图像下,HR图像的条件概率分布\(p_{\mathbf{y|x}}(\mathbf{y|x,\theta})\)。提供的训练数据是LR-HR图像对\(\{(\mathbf{x}_{i},\mathbf{y}_{i})\}_{i = 1}^{M}\)
根据标准化流的思想,要使用一个可逆神经网络\(f_{\theta}\)去拟合这个分布\(p_{\mathbf{y|x}}\),\(f_{\theta}\)把一个HR-LR图像对映射到一个隐变量\(z\)上:\(\mathbf{z} = f_{\theta}(\mathbf{y;x})\)。而要求这个网络在任意\(\mathbf{x}\)的条件下,对于\(\mathbf{y}\)是可逆的,即\(\mathbf{y} = f_{\theta}^{- 1}(\mathbf{z;x})\)。使用概率论中的随机变量代换,可以得到以下式子:
\[ p_{\mathbf{y} \mid \mathbf{x}}(\mathbf{y} \mid \mathbf{x},\mathbf{\theta}) = p_{\mathbf{z}}\left( f_{\mathbf{\theta}}(\mathbf{y};\mathbf{x}) \right)\left| \det\frac{\partial f_{\mathbf{\theta}}}{\partial\mathbf{y}}(\mathbf{y};\mathbf{x}) \right| \] 也就是给定HR图像\(\mathbf{y}\)和LR图像\(\mathbf{x}\),最大化这个\(p_{\mathbf{y} \mid \mathbf{x}}(\mathbf{y} \mid \mathbf{x},\mathbf{\theta})\)就可。写成负对数:
\[ \mathcal{L}(\mathbf{\theta};\mathbf{x},\mathbf{y}) = - \log p_{\mathbf{y} \mid \mathbf{x}}(\mathbf{y} \mid \mathbf{x},\mathbf{\theta}) = - \log p_{\mathbf{z}}\left( f_{\mathbf{\theta}}(\mathbf{y};\mathbf{x}) \right) - \log\left| \det\frac{\partial f_{\mathbf{\theta}}}{\partial\mathbf{y}}(\mathbf{y};\mathbf{x}) \right| \]
即可作为损失函数进行训练了。要想在拟合的分布中采样也很简单,就使用符合预定的分布的\(\mathbf{z}\)代入\(\mathbf{y} = f_{\mathbf{\theta}}^{- 1}(\mathbf{z};\mathbf{x})\)即可。
把以上(3)式的第二项改写成每一层可逆模块串接的形式:
\[ \mathcal{L}(\mathbf{\theta};\mathbf{x},\mathbf{y}) = - \log p_{\mathbf{z}}(\mathbf{z}) - \sum_{n = 0}^{N - 1}\log\left| \det\frac{\partial f_{\mathbf{\theta}}^{n}}{\partial\mathbf{h}^{n}}\left( \mathbf{h}^{n};g_{\mathbf{\theta}}(\mathbf{x}) \right) \right| \]
其中,\(\mathbf{h}^{n + 1} = f_{\mathbf{\theta}}^{n}\left( \mathbf{h}^{n};g_{\mathbf{\theta}}(\mathbf{x}) \right)\),且\(\mathbf{h}^{0} = \mathbf{y}\)、\(\mathbf{h}^{N} = \mathbf{z}\)。这样,只需在每一层上计算特定的雅克比行列式,而不是全体一起计算。而且加入了一个CNN网络\(g_{\theta}\)来学习LR图像最适合作为条件的表示。
条件流层(Conditional Flow Layers)
条件仿射耦合(Conditional Affine Coupling)
\[ \mathbf{h}_{A}^{n + 1} = \mathbf{h}_{A}^{n},\quad\mathbf{h}_{B}^{n + 1} = \exp\left( f_{\mathbf{\theta},\mathbf{s}}^{n}\left( \mathbf{h}_{A}^{n};\mathbf{u} \right) \right) \cdot \mathbf{h}_{B}^{n} + f_{\mathbf{\theta},\mathbf{b}}^{n}\left( \mathbf{h}_{A}^{n};\mathbf{u} \right) \]
\(\mathbf{h}^{n} = \left( \mathbf{h}_{A}^{n},\mathbf{h}_{B}^{n} \right)\)是特征图,A和B是其通道上的分离。这样就能通过仿射变换实现可逆。同时,雅克比矩阵是一个三角阵,他的行列式的对数形式容易写成\(\sum_{\text{ijk}}^{}f_{\mathbf{\theta},s}^{n}\left( \mathbf{h}_{A}^{n};\mathbf{u} \right)_{\text{ijk}}\)
仿射注入(Affine Injector)
对于上一节的设计,要求\(f_{\mathbf{\theta}}^{n}\)是可逆的,而且可以处理雅克比行列式。于是作者做了以下设计,称之为仿射注入器(Affine Injector):
\[ \mathbf{h}^{n + 1} = \exp\left( f_{\mathbf{\theta},s}^{n}(\mathbf{u}) \right) \cdot \mathbf{h}^{n} + f_{\mathbf{\theta},b}(\mathbf{u}) \]
其中\(\mathbf{u} = g_{\theta}(\mathbf{x})\),易得其实可逆的:\(\mathbf{h}^{n} = \exp\left( - f_{\mathbf{\theta},s}^{n}(\mathbf{u}) \right) \cdot \left( \mathbf{h}^{n + 1} - f_{\mathbf{\theta},b}^{n}(\mathbf{u}) \right)\)
同时,雅克比矩阵是一个三角阵,他的行列式的对数形式容易写成\(\sum_{\text{ijk}}^{}f_{\mathbf{\theta},s}^{n}\left( \mathbf{h}_{A}^{n};\mathbf{u} \right)_{\text{ijk}}\)
网络结构
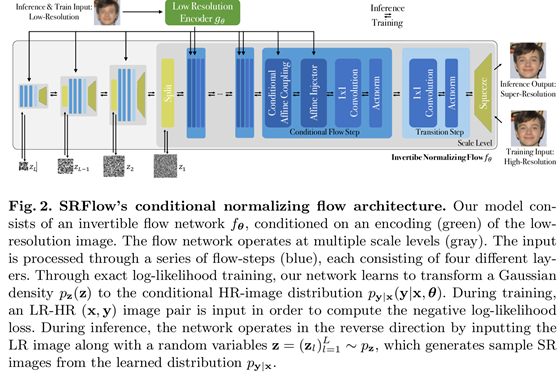
其他的应用
LR一致的Style Transfer
即把一张HR图像下采样成LR图像,进而控制隐变量\(\mathbf{z}\)转移成不同风格的HR图像
Latent Space Normalization
在上述的SR任务中,核心是:把任意符合给定要求("要求"即LR图像)的HR图像映射到一个隐含空间(即z),而为了匹配LR图像中那些"共有的低频特征",这个z被"标准化"为某一分布。
作者提出,原始的\(\widetilde{\mathcal{Z}}\)可以被标准化为另外一个分布\(\widehat{\mathcal{Z}}\):
\[ \widehat{z} = \frac{\widehat{\sigma}}{\widetilde{\sigma}}(\widetilde{z} - \widetilde{\mu}) + \widehat{\mu},\quad\forall\widetilde{z} \in \widetilde{\mathcal{Z}} \]
其中\(\widetilde{\sigma}\)与\(\widetilde{\mu}\)是原始分布的经验标准差和经验均值。进而通过逆过程实现图像风格的迁移\(\widehat{\mathbf{y}} = f_{\mathbf{\theta}}^{- 1}(\widehat{\mathbf{z}},\mathbf{x})\)
后面是这种标准化的两个具体应用。
Image Content Transfer
首先有一张待迁移的HR图片\(\mathbf{y}\),我们把它下采样\(\mathbf{x} = d_{\downarrow}(\mathbf{y})\)。然后我们可以直接在\(\mathbf{y}\)上进行篡改(或许改的很拙劣),得到\(\widetilde{\mathbf{y}}\)。现在我们为了使\(\widetilde{\mathbf{y}}\)看起来不那么拙劣,我们首先把其对应的隐分布表示出来\(\widetilde{\mathbf{z}} = f_{\mathbf{\theta}}(\widetilde{\mathbf{y}};\mathbf{x})\)(注意,这里用到的"要求"是原始的\(\mathbf{y}\)的下采样版本),再使用上述的Latent Space Normalization,从而得到迁移后的图片

Image Restoration
一种使用SR实现图像复原的朴素思想是,利用一些下采样方法,把噪声图像中的噪声去除,再使用SR方法进行复原。但是在下采样的过程中丢失了很多细节。
而使用上述的思想就可以避免这种问题。可以把退化的图像、退化图像的下采样版本都放进\(f_{\theta}\)里:\(\widetilde{\mathbf{z}} = f_{\mathbf{\theta}}(\widetilde{\mathbf{y}};\mathbf{x})\),然后对\(\widetilde{\mathbf{z}}\)进行标准化为\(\widehat{\mathbf{z}}\),进而得到复原的图像\(\widehat{\mathbf{y}} = f_{\mathbf{\theta}}^{- 1}(\widehat{\mathbf{z}},\mathbf{x})\)。完整的复原过程描述为:\(\widehat{\mathbf{y}} = f_{\mathbf{\theta}}^{- 1}\left( \phi\left( f_{\mathbf{\theta}}\left( \widetilde{\mathbf{y}};d_{\downarrow}(\widetilde{\mathbf{y}}) \right) \right),d_{\downarrow}(\widetilde{\mathbf{y}}) \right)\).
直观来说,这个方法是把一个退化图像映射到了分布\(p_{\mathbf{y} \mid \mathbf{x}}(\mathbf{y} \mid \mathbf{x},\mathbf{\theta})\)中最接近的图片,因为这个分布训练的时候,是没有引入退化的,所以就能得到对应的"干净"的HR图片。

实验结果

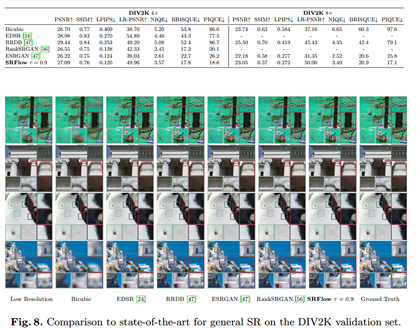

总结与思考
这篇文章与以往大多数超分不一样,它产生的是一个HR图片的分布,而不是单张图片。让我第一次了解到了标准化流的思想,收获很大。
感觉这篇和那篇Invertible Image Rescaling有异曲同工的地方,都使用了一个可逆网络,都是把信息隐藏在一个隐变量中。不同的是,Invertible Image Rescaling是把图像缩小时的丢失的高频信息放在了z中;而本文所求得的"HR图片分布"中的不同样本却对应了同一种z分布,这反映了不同HR样本中的相同的低频内容,从某种意义上是把LR图像中的低频特征放在了z中。
我觉得这篇文章很惊艳的部分在于,利用隐变量的标准化,把这个超分框架推广到了图像风格迁移、图像复原上面。其中"寻找分布\(p_{\mathbf{y} \mid \mathbf{x}}(\mathbf{y} \mid \mathbf{x},\mathbf{\theta})\)中,与目标图像最接近的干净图片"的思想,也非常亮眼。