0%

CodeForce 1324 F：Maximum White Subtree

发表于 分类于 Valine：

求每个节点“最白的”子树

题目链接

https://codeforces.com/contest/1324/problem/F

题意

给\(1,2,3,...,n\)一共\(n\)个点，每个点\(v\)都有一个颜色\(a_v\)——白色(\(a_v=1\))或黑色(\(a_v=0\))。现在用\(n-1\)条边把这\(n\)个点连成一棵树。对于每个点\(v\)，求包含该点\(v\)的所有子树中，\(cnt_{white}-cnt_{black}\)最大的子树，输出该子树对应的\(cnt_{white}-cnt_{black}\)的值。

题解

参考了CF中的Tutorial：

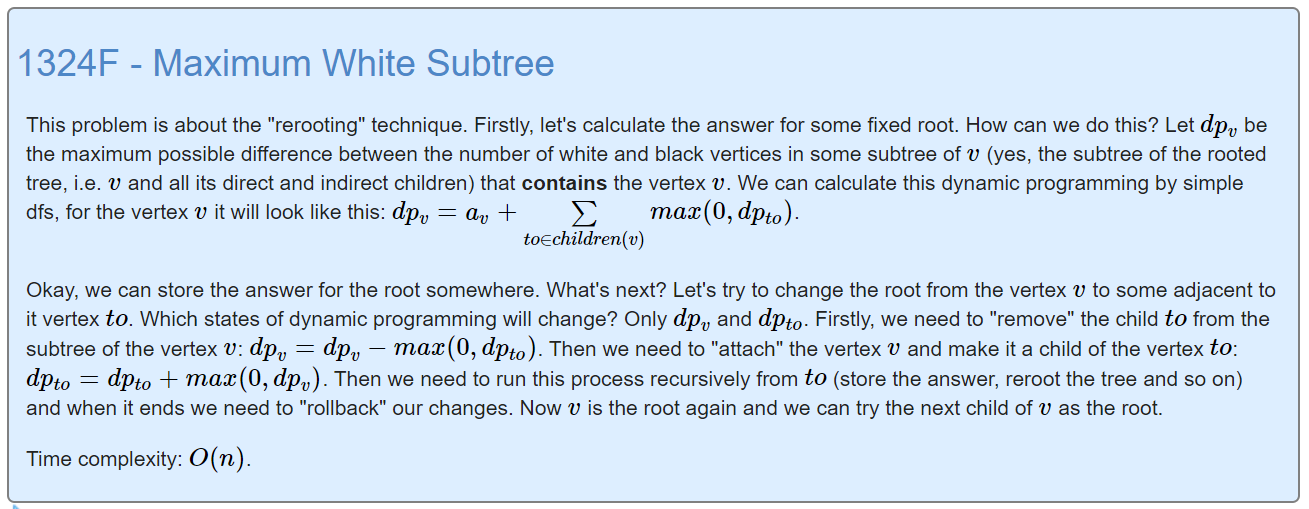
image-20200303201813126

把上述Tutorial中的主要思想阐述如下：

首先，可以把黑点的权值视为-1，白点的权值设为1。因此为方便起见，把数组\(a_1,a_2,...,a_n\)中所有为0的元素都替换成-1。

设\(dp_v\)为顶点\(v\)对应的答案。现在把树想象成，以顶点\(v\)为根的树。这样一来，其余的点都是\(v\)的子节点或是后辈节点。

在将点\(v\)视为树根的前提下，对于任意一点\(u\)，设\(sub^{(v)}_u\)为：当只考虑以\(u\)为根的子树时，点\(u\)对应的答案。显然点\(v\)为根的子树就是整个树，所以\(dp_v=sub^{(v)}_v\)。（括号上标中的\(^{(v)}\)代表是将点\(v\)视为树根的前提下）

对于每个点\(u\)而言，在计算\(sub^{(v)}_u\)的值时，可以对它的每个子节点作考虑，是否要包含其子节点？（注意：这里的“子节点”，还是在将点\(v\)视为树根的前提之下的，并不是点\(v\)的所有邻接点都是其“子节点”。如果\(u\ne v\)，那么\(u\)至少还有个邻接点是\(u\)的“父节点”）

  • 当其子节点\(w\)的\(sub^{(v)}_w\)值大于等于0时，应将以\(w\)为根的子树考虑在内，并将其\(sub^{(v)}_w\)累计进来
  • 当其子节点\(w\)的\(sub^{(v)}_w\)值小于0时，不应将以\(w\)为根的子树考虑在内。

于是，可以得到下列递推式：

\[ 对任意的点u:\ \ \ \ \ sub^{(v)}_u=a_u+\sum_{w\in children_v(u)}{\max (0,sub^{(v)}_w)} \]

这里的\(children_v(u)\)，代表的是：在以\(v\)为树根的意义下，点\(u\)的孩子节点集。

通过一轮从\(v\)开始的DFS搜索，可以自底向上计算出每个节点的\(sub\)值。由于\(dp_v=sub^{(v)}_v\)，这样我们就得到了点\(v\)的答案。此时经过了\(O(n)\)的时间。

如果对\(n\)个点都进行如此的搜索，显然复杂度会达到\(O(n^2)\)级别，肯定会爆T。这时，有一种巧妙的方法。

我们把目光移到点\(v\)的某个邻接点\(to\)这里，先如同求\(dp_v\)的思路一样，把树想象成，以顶点\(to\)为根的树：

\[ dp_{to}=sub^{(to)}_{to}=a_{to}+\sum_{w\in children_{to}(to)}{\max(0,sub^{(to)}_w)} \]

此时，\(to\)的孩子节点\(children_{to}(to)\)中，除了原本就有的孩子之外，还多了上次的\(v\)节点，那么上式可继续写为：

\[ \begin{aligned} dp_{to}=sub^{(to)}_{to}&=a_{to}+\sum_{w\in children_{to}(to)}{\max(0,sub^{(to)}_w)} \\ &=max(0,sub^{(to)}_v)+a_{to}+\sum_{w\in children_{to}(to) \land w\ne v}{\max(0,sub^{(to)}_w)} \end{aligned} \]

上式左边的max函数右侧的\(sub_v^{(to)}\)意为在以\(to\)为根节点前提下，点\(v\)子树对应的答案。这时，相对于上一轮，\(v\)的子树就少了个\(to\)（因为此时\(to\)变成了\(v\)的父节点），于是\(sub_v^{(to)}\)的值，就是上一轮计算的\(dp_v\)减去\(max(0,sub_{to}^{(v)})\)。

最右边那两项\(a_{to}+\sum_{w\in children_{to}(to) \land w\ne v}{\max(0,sub^{(to)}_w)}\)，就是上一轮算\(dp_v\)时计算的\(sub^{(v)}_{to}\)，而这个值是可以事先保存起来的的。那么上式可以继续推导：

\[ \begin{aligned} dp_{to}=sub^{(to)}_{to}&=a_{to}+\sum_{w\in children_{to}(to)}{\max(0,sub^{(to)}_w)} \\ &=max(0,sub^{(to)}_v)+a_{to}+\sum_{w\in children_{to}(to) \land w\ne v}{\max(0,sub^{(to)}_w)} \\ &=max(0,dp_v-max(0,sub^{(v)}_{to}))+sub^{(v)}_{to} \end{aligned} \]

即：

\[ dp_{to}=max(0,dp_v-max(0,sub^{(v)}_{to}))+sub^{(v)}_{to} \]

这样，只需利用上一轮计算出的\(dp_v\)以及\(sub^{(v)}_{to}\)，即可在\(O(1)\)的时间里计算出\(v\)的任意邻接点\(to\)对应的答案\(dp_{to}\)。以此类推，按照同样的DFS的顺序，可以计算出每个点的\(dp\)答案值。

值得注意的是，对于每个点\(w\)而言，每当其父节点\(v'\)的\(dp_{v'}\)值被计算出来，该点的答案\(dp_w\)就能按照下式被计算出来：

\[ dp_{w}=max(0,dp_{v'}-max(0,sub^{({v'})}_{w}))+sub^{({v'})}_{w} \]

而显然，无论以\(v'\)点为根，还是作为其最终祖先\(v\)为根，\(sub^{(v')}_w\)和\(sub^{(v)}_w\)的意义都是相同的，于是对于任意的节点\(w\)，都能以最初的\(sub^{(v)}_w\)参与计算。

将第二次DFS过程中的递推式描述如下：

\[ 对任意 w\ne v\ \ \ \ \ dp_w=max(0,dp_{DFSfather(w)}-max(0,sub^{(v)}_{w}))+sub^{(v)}_{w} \] \(DFSfather(w)\)代表在DFS过程中，\(w\)的父节点。这样，再经过\(O(n)\)的时间，就可以计算出全部答案，总的时间复杂度为\(O(n)+O(n)=O(n)\)

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
#define MAX 200000
vector<int> G[MAX + 5];
int color[MAX + 5];
int n;

int val_1[MAX + 5];
int val_2[MAX + 5];
bool visit[MAX + 5];

int dfs1(int v) {
    
    visit[v] = true;
    int res = color[v];
    for (int i = 0; i < (int)(G[v].size()); i++) {
        if (!visit[G[v][i]])
            res += max(0, dfs1(G[v][i]));
    }
    val_1[v] = res;
    return res;
}

void dfs2(int v, int father) {
    
    visit[v] = true;
    // val_2[v] = val_1[v] >= 0 ? val_1[v] + max(0, val_2[father] - val_1[v]) : val_1[v] + max(0, val_2[father]);
    val_2[v] = max(0, val_2[father] - max(0, val_1[v])) + val_1[v]; 
    for (int i = 0; i < (int)(G[v].size()); i++) {
        if (!visit[G[v][i]])
            dfs2(G[v][i], v);
    }
}

int main() {
    memset(visit, false, sizeof(visit));
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        int c;
        scanf("%d", &c);
        color[i] = c == 0 ? -1 : c;
    }
    for (int i = 0; i < n - 1; i++) {
        int v, u;
        scanf("%d %d", &v, &u);
        G[v].push_back(u);
        G[u].push_back(v);
    }

    val_2[1] = dfs1(1);
    memset(visit, false, sizeof(visit));

    visit[1] = true;
    for (int i = 0; i < (int)(G[1].size()); i++) {
        dfs2(G[1][i], 1);
    }

    for (int i = 1; i <= n; i++) {
        printf("%d ", val_2[i]);
    }
    printf("\n");
    return 0;
}